
【题目】如图,点O为直线AB上一点,过点O作射线OC,将一直角三角板按图中所示的方式摆放(∠MON=900)
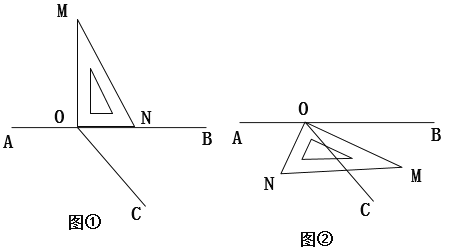
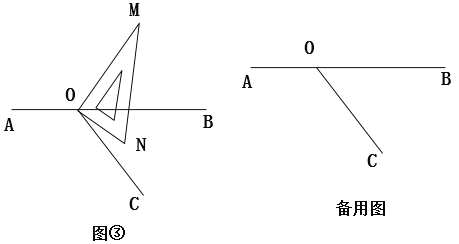
探究一:将图①中的三角板绕点0顺时针方向旋转一定的角度得到图②,使边OM恰好平分∠BOC。若∠BOC=500,ON是否平分∠A0C? 请说明理由;
探究二:将图①中的三角板绕点O时针旋转一定的角度得到图③,
(1)使边ON在∠BOC的内部,如果∠BOC=600,则∠BOM与∠CON之间存在怎样的数量关系?请说明理由。
(2)使边ON在∠BOC的内部,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
【答案】探究一、ON平分∠AOC,理由见解析;探究二、(1)∠BOM-∠CON=300 ,理由见解析;(2)∠BOM=∠NOC+30°, 理由见解析.
【解析】
探究一:角平分线的定义可知∠BOM=∠MOC,由∠NOM=90°,可知∠BOM+∠AON=90°,∠MOC+∠NOC=90°,根据等角的余角相等可知∠AON=∠NOC;
探究二:(1)根据题意可知∠NOC+∠NOB=60°,∠BOM+∠NOB=90°,由∠BOM=90°∠NOB、∠BON=60°∠NOC可得到∠BOM=∠NOC+30°.
(2)根据∠CON+∠NOB=60°、∠BOM+∠NOB=90°可得∠BOM=∠NOC+30°.
解:探究一、ON平分∠AOC,
理由如下:∵OM平分∠BOC,且∠BOC=50°
∴∠BOM=∠COM=25°
∵∠MON=90°
∴∠CON=90°-25°=65°
∵∠AON=180°-90°-25°=65°
∴∠CON=∠AON
∴ON平分∠AOC
探究二、(1)∠BOM-∠CON=30°
∵∠MON=90°
∴∠BON=90°-∠BOM
∵∠BOC=60°
∴∠BON=60°-∠CON
∴90°-∠BOM=60°-∠CON
即:∠BOM-∠CON=300 .
(2)∠BOM=∠NOC+30°.理由如下:
∵∠CON+∠NOB=60°,∠BOM+∠NOB=90°
∴∠BOM=∠NOC+30°.



科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠B=30°,点D在BC上,过点D作DE⊥BC,交BA或其延长线于点E,过点E作EF⊥BA交AC或其延长线于点F,连接DF.若DF⊥AC,则BD=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
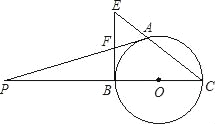
【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P.
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(-2,-1)在它的图像上 B. 它的图像在第一、三象限
C. 当![]() 时,y随x的增大而增大 D. 当
时,y随x的增大而增大 D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】C
【解析】试题分析:反比例函数![]() 的性质:当
的性质:当![]() 时,图象在一、三象限,在每一象限,y随x的增大而减小;当
时,图象在一、三象限,在每一象限,y随x的增大而减小;当![]() 时,图象在二、四象限,在每一象限,y随x的增大而增大.
时,图象在二、四象限,在每一象限,y随x的增大而增大.
A.点![]() 在它的图象上,B.它的图象在第一、三象限,C.当
在它的图象上,B.它的图象在第一、三象限,C.当![]() 时,
时,![]() 随
随![]() 的增大而减小,均正确,不符合题意;
的增大而减小,均正确,不符合题意;
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小,故错误,本选项符合题意.
的增大而减小,故错误,本选项符合题意.
考点:反比例函数的性质
点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.
【题型】单选题
【结束】
8
【题目】由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
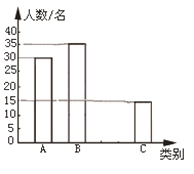
A. 900名 B. 1050名 C. 600名 D. 450名
查看答案和解析>>
科目:初中数学 来源: 题型:
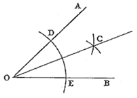
【题目】如图,已知![]() ,小明按如下步骤作图:
,小明按如下步骤作图:
(1)以点O为圆心,适当长为半径画弧,交OA于D,交OB于点E
(2)分别以点D、E为圆心,大于![]() 的长为半径画弧,两弧在
的长为半径画弧,两弧在![]() 的内部相交于点C
的内部相交于点C
(3)画射线OC
根据上述作图步骤,下列结论正确的有( )个
①射线OC是![]() 的平分线;②点O和点C关于直线DE对称;③射线OC垂直平分线段DE;④
的平分线;②点O和点C关于直线DE对称;③射线OC垂直平分线段DE;④![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
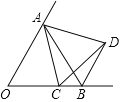
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节即将来临时,某商人抓住商机购进甲、乙、丙三种糖果,已知销售甲糖果的利润率为![]() ,乙糖果的利润率为
,乙糖果的利润率为![]() ,丙糖果的利润率为
,丙糖果的利润率为![]() ,当售出的甲、乙、丙糖果重量之比为
,当售出的甲、乙、丙糖果重量之比为![]() 时,商人得到的总利润率为
时,商人得到的总利润率为![]() ;当售出的甲、乙、丙糖果重量之比为
;当售出的甲、乙、丙糖果重量之比为![]() 时,商人得到的总利率为
时,商人得到的总利率为![]() .那么当售出的甲、乙、丙糖果重量之比为
.那么当售出的甲、乙、丙糖果重量之比为![]() 时,这个商人得到的总利润率为______.
时,这个商人得到的总利润率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com