
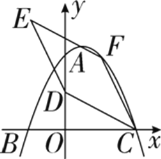
【题目】如图,在平面直角坐标系中,二次函数y=-![]() x2+bx+C的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
x2+bx+C的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
【答案】(1) y=-![]() x2+x+8,C (8,0);(2) ①50;②18.
x2+x+8,C (8,0);(2) ①50;②18.
【解析】
(1)把A点和B点坐标代入y=-![]() x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线的解析式;然后计算函数值为0时对应的自变量的值即可得到C点坐标
(2)①连结DF,OF,如图,设F(t,-![]() t2+t+8),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=-t2+6t+16,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
t2+t+8),利用S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,利用三角形面积公式得到S△CDF=-t2+6t+16,再利用二次函数的性质得到△CDF的面积有最大值,然后根据平行四边形的性质可得S的最大值;
②由于四边形CDEF为平行四边形,则CD∥EF,CD=EF,利用C点和D的坐标特征可判断点C向左平移8个单位,再向上平移4个单位得到点D,则点F向左平移8个单位,再向上平移4个单位得到点E,即E(t-8,-![]() t2+t+12),然后把E(t-8,-
t2+t+12),然后把E(t-8,-![]() t2+t+12)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
t2+t+12)代入抛物线解析式得到关于t的方程,再解方程求出t后计算△CDF的面积,从而得到S的值.
解:(1)∵二次函数y=-![]() x2+Bx+C过A(0,8)、B(-4,0)两点,
x2+Bx+C过A(0,8)、B(-4,0)两点,
∴![]() ,解得
,解得![]() ,
,
∴二次函数的解析式为y=-![]() x2+x+8,
x2+x+8,
当y=0时,解得x1=-4,x2=8,
∴C点坐标为(8,0);
(2)①如解图,连接DF,OF,设F(M,-![]() M2+M+8),
M2+M+8),
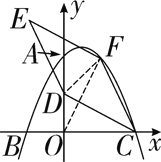
∵S四边形OCFD=S△CDF+S△OCD=S△ODF+S△OCF,
∴S△CDF=S△ODF+S△OCF-S△OCD,
=![]() ×4×M+
×4×M+![]() ×8×(-
×8×(-![]() M2+M+8)-
M2+M+8)-![]() ×8×4
×8×4
=2M-M2+4M+32-16
=-M2+6M+16
=-(M-3)2+25,
当M=3时,△CDF的面积有最大值,最大值为25,
∵四边形CDEF为平行四边形,
∴S四边形CDEF=2S△CDF=50,
∴S的最大值为50;
②S=18.
∵四边形CDEF为平行四边形,
∴CD∥EF,CD=EF,
∵点C向左平移8个单位,再向上平移4个单位得到点D,
∴点F向左平移8个单位,再向上平移4个单位得到点E,即E(M-8,-![]() M2+M+12),
M2+M+12),
∵E(M-8,-![]() M2+M+12)在抛物线上,
M2+M+12)在抛物线上,
∴-![]() (M-8)2+(M-8)+8=-
(M-8)2+(M-8)+8=-![]() M2+M+12,
M2+M+12,
解得M=7,
当M=7时,S△CDF=-(7-3)2+25=9,
∴此时S=2S△CDF=18.


科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某隧道洞的内部截面顶部是抛物线形,现测得地面宽 AB=10m,隧道顶点O到地面AB的距离为5m,
(1)建立适当的平面直角坐标系,幵求该抛物线的解析式;
(2)一辆小轿车长 4.5米,宽2米,高1.5米,同样大小的小轿车通过该隧道,最多能有 几辆车幵行?
查看答案和解析>>
科目:初中数学 来源: 题型:
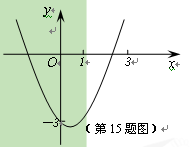
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
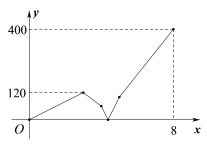
【题目】在一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止.在甲车出发的同时,乙车也从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶.若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在两车出发后经过_____小时相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为![]() 元,则可卖出(350-10
元,则可卖出(350-10![]() )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过y轴上一个动点M作x轴的平行线,交双曲线y=![]() 于点A,交双曲线
于点A,交双曲线![]() 于点B,点C、点D在x轴上运动,且始终保持DC=AB,则平行四边形ABCD的面积是( )
于点B,点C、点D在x轴上运动,且始终保持DC=AB,则平行四边形ABCD的面积是( )
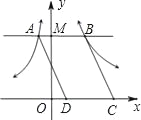
A. 7 B. 10 C. 14 D. 28
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com