
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和半径为1的
和半径为1的![]() ,定义如下:
,定义如下:
①点![]() 的“派生点”为
的“派生点”为![]() ;
;
②若![]() 上存在两个点
上存在两个点![]() ,使得
,使得![]() ,则称点
,则称点![]() 为
为![]() 的“伴侣点”.
的“伴侣点”.
应用:已知点![]()
(1)点![]() 的派生点
的派生点![]() 坐标为________;在点
坐标为________;在点![]() 中,
中,![]() 的“伴侣点”是________;
的“伴侣点”是________;
(2)过点![]() 作直线
作直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,使
,使![]() ,若直线
,若直线![]() 上的点
上的点![]() 是
是![]() 的“伴侣点”,求
的“伴侣点”,求![]() 的取值范围;
的取值范围;
(3)点![]() 的派生点
的派生点![]() 在直线
在直线![]() ,求点
,求点![]() 与
与![]() 上任意一点距离的最小值.
上任意一点距离的最小值.
【答案】(1)(1,0),E、D、![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
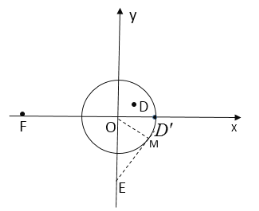
(1)根据定义即可得到点![]() 的坐标,过点E作
的坐标,过点E作![]() 的切线EM,连接OM,利用三角函数求出∠MEO=30°,即可得到点E是
的切线EM,连接OM,利用三角函数求出∠MEO=30°,即可得到点E是![]() 的“伴侣点”;根据点F、D、
的“伴侣点”;根据点F、D、![]() 的坐标得到线段长度与线段OE比较即可判定是否是
的坐标得到线段长度与线段OE比较即可判定是否是![]() 的“伴侣点”;
的“伴侣点”;
(2)根据题意求出![]() ,∠OGF=60°,由点
,∠OGF=60°,由点![]() 是
是![]() 的“伴侣点”,过点P作
的“伴侣点”,过点P作![]() 的切线PA、PB,连接OP,OB,证明△OPG是等边三角形,得到点P应在线段PG上,过点P作PH⊥x轴于H,求出点P的横坐标是-
的切线PA、PB,连接OP,OB,证明△OPG是等边三角形,得到点P应在线段PG上,过点P作PH⊥x轴于H,求出点P的横坐标是-![]() ,由此即可得到点P的横坐标m的取值范围;
,由此即可得到点P的横坐标m的取值范围;
(3)设点![]() (x,-2x+6),P(m,n),根据派生点的定义得到3m+n=6,由此得到点P在直线y=-3x+6上,设直线y=-3x+6与x轴交于点A,与y轴交于点B,过点O作OH⊥AB于H,交
(x,-2x+6),P(m,n),根据派生点的定义得到3m+n=6,由此得到点P在直线y=-3x+6上,设直线y=-3x+6与x轴交于点A,与y轴交于点B,过点O作OH⊥AB于H,交![]() 于点C,求出AB的长,再根据面积公式求出OH即可得到答案.
于点C,求出AB的长,再根据面积公式求出OH即可得到答案.
(1)∵![]() ,
,
∴点![]() 的派生点
的派生点![]() 坐标为(1,0),
坐标为(1,0),
∵E(0,-2),
∴OE=2,
过点E作![]() 的切线EM,连接OM,
的切线EM,连接OM,
∵OM=1,OE=2,∠OME=90°,
∴sin∠MEO=![]() ,
,
∴∠MEO=30°,
而在![]() 的左侧也有一个切点,使得组成的角等于30°,
的左侧也有一个切点,使得组成的角等于30°,
∴点E是![]() 的“伴侣点”;
的“伴侣点”;
∵![]() ,
,
∴OF=![]() >OE,
>OE,
∴点F不可能是![]() 的“伴侣点”;
的“伴侣点”;
∵![]() ,
,![]() (1,0),
(1,0),![]() ,
,![]() ,
,
∴点D、![]() 是
是![]() 的“伴侣点”,
的“伴侣点”,
∴![]() 的“伴侣点”有:E、D、
的“伴侣点”有:E、D、![]() ,
,
故答案为:(1,0),E、D、![]() ;
;
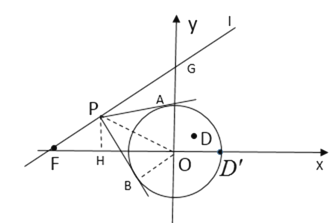
(2)如图,直线l交y轴于点G,
∵![]() ,
,
∴![]() ,∠OGF=60°
,∠OGF=60°
∵直线![]() 上的点
上的点![]() 是
是![]() 的“伴侣点”,
的“伴侣点”,
∴过点P作![]() 的切线PA、PB,且∠APB=60°,
的切线PA、PB,且∠APB=60°,
连接OP,OB,
∴∠BOP=30°,
∵∠OBP=90°,OB=1,
∴OP=2=OG,
∴△OPG是等边三角形,
∴若点P是![]() 的“伴侣点”,则点P应在线段PG上,
的“伴侣点”,则点P应在线段PG上,
过点P作PH⊥x轴于H,
∵∠POH=90°-60°=30°,OP=2,
∴PH=1,
∴OH=![]() ,即点P的横坐标是-
,即点P的横坐标是-![]() ,
,
∴当直线![]() 上的点
上的点![]() 是
是![]() 的“伴侣点”时
的“伴侣点”时![]() 的取值范围是
的取值范围是![]() ;
;
(3)设点![]() (x,-2x+6),P(m,n),
(x,-2x+6),P(m,n),
根据题意得:m+n=x,m-n=-2x+6,
∴3m+n=6,
即n=-3m+6,
∴点P坐标为(m,-3m+6),
∴点P在直线y=-3x+6上,
设直线y=-3x+6与x轴交于点A,与y轴交于点B,过点O作OH⊥AB于H,交![]() 于点C,如图,则A(2,0),B(0,6),
于点C,如图,则A(2,0),B(0,6),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即点P与![]() 上任意一点距离的最小值为
上任意一点距离的最小值为![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.
(1)如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为_____;
(2)如图2,当PB=5时,若直线l//AC,则BB’的长度为 ;
(3)如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题是真命题的是( )
A.两直线平行,同位角相等
B.等边三角形是锐角三角形
C.如果两个实数是正数,那么它们的积是正数
D.全等三角形的对应角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
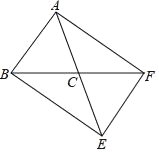
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
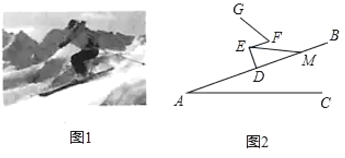
【题目】图1,图2分别是一滑雪运动员在滑雪过程中某一时刻的实物图与示意图,已知运动员的小腿![]() 与斜坡
与斜坡![]() 垂直,大腿
垂直,大腿![]() 与斜坡
与斜坡![]() 平行,且
平行,且![]() 三点共线,若雪仗
三点共线,若雪仗![]() 长为
长为![]() ,
,![]() ,
,![]() ,求此刻运动员头部
,求此刻运动员头部![]() 到斜坡
到斜坡![]() 的高度
的高度![]() (精确到
(精确到![]() )(参考数据:
)(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.
(1)设花圃的一边AB长为x米,请你用含x的代数式表示另一边AD的长为 米;
(2)若此时花圃的面积刚好为45m2,求此时花圃的长与宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
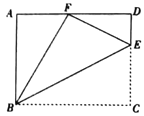
【题目】如图,点![]() 是矩形
是矩形![]() 中
中![]() 边上一点,
边上一点,![]() 沿
沿![]() 折叠为
折叠为![]() ,点
,点![]() 落在
落在![]() 上.
上.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,是否存在
,是否存在![]() 的值,使
的值,使![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
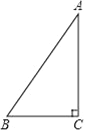
【题目】如图,在△ABC 中,∠C=90°
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE
①求证:CD=DE;
②若sinA=![]() ,AC=6,求AD.
,AC=6,求AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.
S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com