
【题目】如图,点![]() 是矩形
是矩形![]() 中
中![]() 边上一点,
边上一点,![]() 沿
沿![]() 折叠为
折叠为![]() ,点
,点![]() 落在
落在![]() 上.
上.
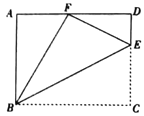
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,是否存在
,是否存在![]() 的值,使
的值,使![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一段抛物线;![]() ,记为
,记为![]() 它与
它与![]() 轴交于点
轴交于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ;将
;将![]() ,绕点
,绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ,……,若
,……,若![]() 是其中某段抛物线上一点,则
是其中某段抛物线上一点,则![]() __________.
__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形 ABCD 中,E 为边 BC 上一点,F 为边 CD 上一点,且∠AEF=90°.
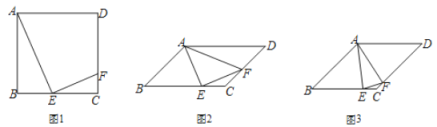
(1)如图 1,若 ABCD 为正方形,E 为 BC 中点,求证:![]() .
.
(2)若 ABCD 为平行四边形,∠AFE=∠ADC,
①如图 2,若∠AFE=60°,求![]() 的值;
的值;
②如图 3,若 AB=BC,EC=2CF.直接写出 cos∠AFE 值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和半径为1的
和半径为1的![]() ,定义如下:
,定义如下:
①点![]() 的“派生点”为
的“派生点”为![]() ;
;
②若![]() 上存在两个点
上存在两个点![]() ,使得
,使得![]() ,则称点
,则称点![]() 为
为![]() 的“伴侣点”.
的“伴侣点”.
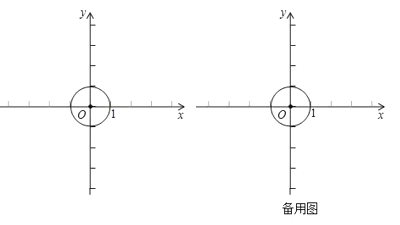
应用:已知点![]()
(1)点![]() 的派生点
的派生点![]() 坐标为________;在点
坐标为________;在点![]() 中,
中,![]() 的“伴侣点”是________;
的“伴侣点”是________;
(2)过点![]() 作直线
作直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,使
,使![]() ,若直线
,若直线![]() 上的点
上的点![]() 是
是![]() 的“伴侣点”,求
的“伴侣点”,求![]() 的取值范围;
的取值范围;
(3)点![]() 的派生点
的派生点![]() 在直线
在直线![]() ,求点
,求点![]() 与
与![]() 上任意一点距离的最小值.
上任意一点距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ADE中,∠DAE=90°,C是边AE上任意一点(点C与点A、E不重合),以AC为一直角边在Rt△ADE的外部作Rt△ABC,∠BAC=90°,连接BE、CD.
(1)在图1中,若AC=AB,AE=AD,现将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图2,那么线段BE.CD之间有怎样的关系,写出结论,并说明理由;
(2)在图1中,若CA=3,AB=5,AE=10,AD=6,将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图3,连接BD、CE.
①求证:△ABE∽△ACD;
②计算:BD2+CE2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查了部分学生的数学成绩,并将抽样的数据进行了如下整理.
(1)填空![]() _______,
_______,![]() _______,数学成绩的中位数所在的等级_________.
_______,数学成绩的中位数所在的等级_________.
(2)如果该校有1200名学生参加了本次模拟测,估计![]() 等级的人数;
等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A级学生的数学成绩的平均分数.
①如下分数段整理样本
等级等级 | 分数段 | 各组总分 | 人数 |
|
|
| 4 |
|
| 843 |
|
|
| 574 |
|
|
| 171 | 2 |
②根据上表绘制扇形统计图
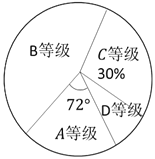
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中作图:①分别以点B,C为圆心,BC长为半径画弧,分别交AD于点H,G;②分别以点B,C为圆心,大于BC的一半长为半径画弧,两弧相交于点E,F;③作直线EF,交AD于点P.下列结论不一定成立的是( )

A.BC=BHB.CG=AD
C.PB=PCD.GH=2AB
查看答案和解析>>
科目:初中数学 来源: 题型:
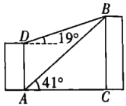
【题目】如图,已知一居民楼![]() 前方
前方![]() 处有一建筑物
处有一建筑物![]() ,小敏在居民楼的顶部
,小敏在居民楼的顶部![]() 处和底部
处和底部![]() 处分别测得建筑物顶部
处分别测得建筑物顶部![]() 的仰角为
的仰角为![]() 和
和![]() ,求居民楼的高度
,求居民楼的高度![]() 和建筑物的高度
和建筑物的高度![]() (结果取整数).
(结果取整数).
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com