
【题目】四边形 ABCD 中,E 为边 BC 上一点,F 为边 CD 上一点,且∠AEF=90°.
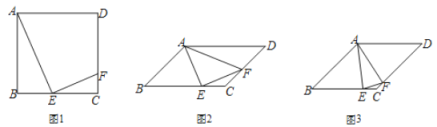
(1)如图 1,若 ABCD 为正方形,E 为 BC 中点,求证:![]() .
.
(2)若 ABCD 为平行四边形,∠AFE=∠ADC,
①如图 2,若∠AFE=60°,求![]() 的值;
的值;
②如图 3,若 AB=BC,EC=2CF.直接写出 cos∠AFE 值为 .
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】
(1)如图1中,设正方形的边长为2a.只要证明△ABE∽△ECF,可得![]() ,求出CF、DF即可解决问题;
,求出CF、DF即可解决问题;
(2)如图2中,在AD上取一点H,使得FH=DF.只要证明△AEF是等边三角形,推出AF=2EF,再证明△AHF∽△FCE,可得EC:HF=EF:AF=1:2;
(3)如图3,作FT=FD交AD于点T,作FH⊥AD于H,证△FCE∽△ATF,设CF=2,则CE=4,可设AT=x,则TF=2x,AD=CD=2x+2,DH=![]() DT=
DT=![]() ,分别用含x的代数式表示出∠AFE和∠D的余弦值,列出方程,求出x的值,即可求出结论.
,分别用含x的代数式表示出∠AFE和∠D的余弦值,列出方程,求出x的值,即可求出结论.
(1)证明:如图1中,设正方形的边长为2a.
∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,∠FEC+∠EFC=90°,
∴∠AEB=∠EFC,
∴△ABE∽△ECF,
∴![]()
∵BE=EC=a,AB=CD=2a,
∴CF=![]() a,DF=CDCF=
a,DF=CDCF=![]() a,
a,
∴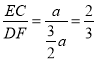 ;
;
(2)如图2中,在AD上取一点H,使得FH=DF,
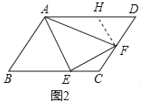
∵∠AEF=90°,∠AFE=∠D=60°,
∴AF=2EF,
∵FH=DF,
∴△DHF是等边三角形,
∴∠FHD=60°,
∴∠AHF=120°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C=180°∠D=120°,
∴∠AHF=∠C,
∵∠AFC=∠D+∠FAH=∠EFC+∠AFE,∠AFE=∠D,
∴∠HAF=∠EFC,
∴△AHF∽△FCE,
∴EC:HF=EF:AF=1:2,
∴![]() ;
;
如图3,作FT=FD交AD于点T,作FH⊥AD于H
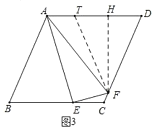
则∠FTD=∠FDT,
∴180°∠FTD=180°∠D,
∴∠ATF=∠C,
又∵∠TAF+∠D=∠AFE+∠CFE,且∠D=∠AFE,
∴∠TAF=∠CFE,
∴△FCE∽△ATF,
∴![]() =
=![]() ,
,
设CF=2,则CE=4,可设AT=x,则TF=2x,AD=CD=2x+2,
∴DH=![]() DT=
DT=![]() ,且
,且![]() ,
,
由cos∠AFE=cos∠D,得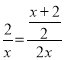 ,
,
解得x=6,(x=0舍去)
∴cos∠AFE=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
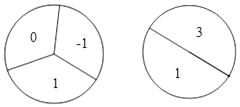
【题目】小明做游戏:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘的指针所指数字都为x2﹣4x+3=0的根时,他就可以获得一次为大家表演节目的机会.
(1)利用树状图或列表的方法(只选一种)表示出游戏可能出现的所有结果;
(2)求小明参加一次游戏就为大家表演节目的机会的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题是真命题的是( )
A.两直线平行,同位角相等
B.等边三角形是锐角三角形
C.如果两个实数是正数,那么它们的积是正数
D.全等三角形的对应角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
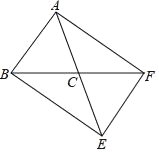
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
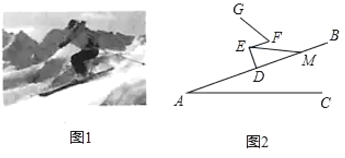
【题目】图1,图2分别是一滑雪运动员在滑雪过程中某一时刻的实物图与示意图,已知运动员的小腿![]() 与斜坡
与斜坡![]() 垂直,大腿
垂直,大腿![]() 与斜坡
与斜坡![]() 平行,且
平行,且![]() 三点共线,若雪仗
三点共线,若雪仗![]() 长为
长为![]() ,
,![]() ,
,![]() ,求此刻运动员头部
,求此刻运动员头部![]() 到斜坡
到斜坡![]() 的高度
的高度![]() (精确到
(精确到![]() )(参考数据:
)(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
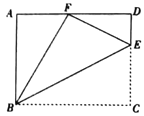
【题目】如图,点![]() 是矩形
是矩形![]() 中
中![]() 边上一点,
边上一点,![]() 沿
沿![]() 折叠为
折叠为![]() ,点
,点![]() 落在
落在![]() 上.
上.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,是否存在
,是否存在![]() 的值,使
的值,使![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平行四边形![]() 中,点
中,点![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 于点
于点![]() ,
,
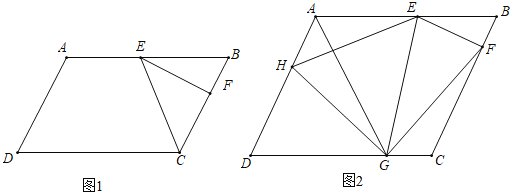
(1)如图1,连接![]() ,若点
,若点![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(2)如图2,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 为等边三角形,且
为等边三角形,且![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com