
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的
,以AB为直径的![]() 分别与
分别与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
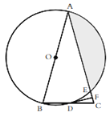
(1)求证:DF是![]() 的切线;
的切线;
(2)若![]() 的半径为3,
的半径为3,![]() ,求阴影部分的面积;
,求阴影部分的面积;
(3)求证:![]() .
.
【答案】(1)见解析;(2)阴影部分的面积是![]() ; (3)见解析.
; (3)见解析.
【解析】
(1)连接OD,求出AC∥OD,可得OD⊥DF,根据切线的判定可得结论;
(2)连接OE,过O作OM⊥AC于M,根据含30度直角三角形的性质求出AE、OM的长和∠AOE的度数,然后根据阴影部分的面积=S扇形AOES△AOE进行计算;
(3)连接BE,AD,DE,根据平行线的性质和圆周角定理求出∠FDC=∠DAC,然后求出∠DEC=∠C,根据三线合一得到∠EDF=∠FDC,即可证明结论.
解:(1)连接OD,
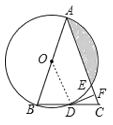
∵AB=AC,OB=OD,
∴∠ABC=∠C,∠ABC=∠ODB,
∴∠ODB=∠C,
∴AC∥OD,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE,过O作OM⊥AC于M,则∠AMO=90°,
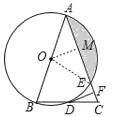
∵DF⊥AC,
∴∠DFC=90°,
∵∠FDC=15°,
∴∠C=180°90°15°=75°,
∴∠ABC=∠C=75°,
∴∠BAC=180°∠ABC∠C=30°,
∴OM=![]() OA=
OA=![]() ×3=
×3=![]() ,AM=
,AM=![]() ,
,
∵OM⊥AC,
∴AE=2AM=![]() ,
,
∵∠BAC=∠AEO=30°,
∴∠AOE=180°30°30°=120°,
∴阴影部分的面积=S扇形AOES△AOE=![]() ;
;
(3)连接BE,AD,DE,
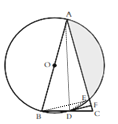
∵AB为⊙O的直径,
∴∠AEB=90°,
∴BE⊥AC,
∵DF⊥AC,
∴BE∥DF,
∴∠FDC=∠EBC,
∵∠EBC=∠DAC,
∴∠FDC=∠DAC,
∵A、B、D、E四点共圆,
∴∠DEF=∠ABC,
∵∠ABC=∠C,
∴∠DEC=∠C,
∵DF⊥AC,
∴∠EDF=∠FDC,
∴∠EDF=∠DAC.


科目:初中数学 来源: 题型:
【题目】背景知识:如图,在![]() 中,
中,![]() ,若
,若![]() ,则:
,则:![]() .
.
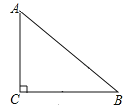
(1)解决问题:
如图(1),![]() ,
,![]() ,
,![]() 是过点
是过点![]() 的直线,过点
的直线,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,现尝试探究线段
,现尝试探究线段![]() 、
、![]() 、
、![]() 之间的数量关系:过点
之间的数量关系:过点![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,易发现图中出现了一对全等三角形,即
,易发现图中出现了一对全等三角形,即![]() ,由此可得线段
,由此可得线段![]() 、
、![]() 、
、![]() 之间的数量关系是: ;
之间的数量关系是: ;

(2)类比探究:
将图(1)中的![]() 绕点
绕点![]() 旋转到图(2)的位置,其它条件不变,试探究线段
旋转到图(2)的位置,其它条件不变,试探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(3)拓展应用:
将图(1)中的![]() 绕点
绕点![]() 旋转到图 (3)的位置,其它条件不变,若
旋转到图 (3)的位置,其它条件不变,若![]() ,
,![]() ,则
,则![]() 的长为 (直接写结果).
的长为 (直接写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子中有1个红球,1个白球和2个蓝球,这些球除颜色外都相同,从中随机摸出1个球,记下颜色后放回,再从中随机摸出1个球.
![]() 两次摸到相同颜色的球的概率;
两次摸到相同颜色的球的概率;
![]() 在上面的问题中,如果从中随机摸出1个球,记下颜色后不放回,再从中随机摸出1个球,求两次摸到的球的颜色能配成紫色
在上面的问题中,如果从中随机摸出1个球,记下颜色后不放回,再从中随机摸出1个球,求两次摸到的球的颜色能配成紫色![]() 红色与蓝色配成紫色
红色与蓝色配成紫色![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线;![]() ,记为
,记为![]() 它与
它与![]() 轴交于点
轴交于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ;将
;将![]() ,绕点
,绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ,……,若
,……,若![]() 是其中某段抛物线上一点,则
是其中某段抛物线上一点,则![]() __________.
__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )

A.20海里 B.40海里 C.![]() 海里 D.
海里 D.![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶专营店销售一款牛奶,售价是在进价的基础上加价a%出售,每月的销售额可以达到9.6万元,但每月需支出2.45万元的固定费用及进价的2.5%的其他费用.
(1)如果该款牛奶每月所获的利润要达到1万元,那么a的值是多少?(利润=售价﹣进价﹣固定费用﹣其他费用)
(2)现这款牛奶的售价为64元/盒,根据市场调查,这款牛奶如果售价每降低1%,销售量将上升8%,求这款牛奶调价销售后,每月可获的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖在完成一项“社会调查”作业时,需要调查城市送餐人员的收入情况,他了解到劳务公司为了鼓励送餐员的工作积极性,实行“月总收入![]() 基本工资(固定)
基本工资(固定)![]() 送餐单数奖励”的方法计算薪资,调查中获得如下信息:
送餐单数奖励”的方法计算薪资,调查中获得如下信息:
送餐员 | 小李 | 小杨 |
月送餐单数/单 | 292 | 273 |
月总收入/元 | 3384 | 3346 |
送餐每单奖励![]() 元,送餐员月基本工资为
元,送餐员月基本工资为![]() 元;
元;
(1)求a、b的值;
(2)若月送餐单数超过300单时,超过部分每单的奖金增加1元.假设月送餐单数为![]() 单,月总收入为
单,月总收入为![]() 元,请写出
元,请写出![]() 与
与![]() 的函数关系式,若送餐员小李计划月收入不低于5200元,那么他每月至少要送多少单?
的函数关系式,若送餐员小李计划月收入不低于5200元,那么他每月至少要送多少单?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形 ABCD 中,E 为边 BC 上一点,F 为边 CD 上一点,且∠AEF=90°.
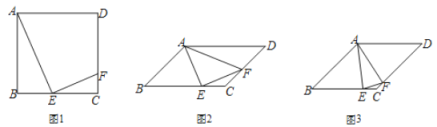
(1)如图 1,若 ABCD 为正方形,E 为 BC 中点,求证:![]() .
.
(2)若 ABCD 为平行四边形,∠AFE=∠ADC,
①如图 2,若∠AFE=60°,求![]() 的值;
的值;
②如图 3,若 AB=BC,EC=2CF.直接写出 cos∠AFE 值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中作图:①分别以点B,C为圆心,BC长为半径画弧,分别交AD于点H,G;②分别以点B,C为圆心,大于BC的一半长为半径画弧,两弧相交于点E,F;③作直线EF,交AD于点P.下列结论不一定成立的是( )

A.BC=BHB.CG=AD
C.PB=PCD.GH=2AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com