
【题目】某品牌牛奶专营店销售一款牛奶,售价是在进价的基础上加价a%出售,每月的销售额可以达到9.6万元,但每月需支出2.45万元的固定费用及进价的2.5%的其他费用.
(1)如果该款牛奶每月所获的利润要达到1万元,那么a的值是多少?(利润=售价﹣进价﹣固定费用﹣其他费用)
(2)现这款牛奶的售价为64元/盒,根据市场调查,这款牛奶如果售价每降低1%,销售量将上升8%,求这款牛奶调价销售后,每月可获的最大利润.
科目:初中数学 来源: 题型:
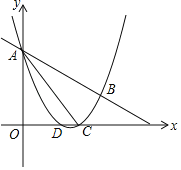
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A,B两点,交x轴与D,C两点,连接AC,已知A(0,3),C(3,0).(1)抛物线的解析式__;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒
交于A,B两点,交x轴与D,C两点,连接AC,已知A(0,3),C(3,0).(1)抛物线的解析式__;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒![]() 个单位的速度运动到A后停止.若使点M在整个运动中用时最少,则点E的坐标__.
个单位的速度运动到A后停止.若使点M在整个运动中用时最少,则点E的坐标__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.
(1)如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为_____;
(2)如图2,当PB=5时,若直线l//AC,则BB’的长度为 ;
(3)如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
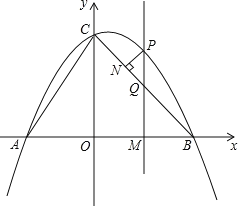
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .点
.点![]() 是第一象限内抛物线上的一个动点,点
是第一象限内抛物线上的一个动点,点![]() 的横坐标为
的横坐标为![]() .
.
(1)求此抛物线的表达式;
(2)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() .试探究点P在运动过程中,是否存在这样的点
.试探究点P在运动过程中,是否存在这样的点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形.若存在,请求出此时点
为顶点的三角形是等腰三角形.若存在,请求出此时点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .请用含
.请用含![]() 的代数式表示线段
的代数式表示线段![]() 的长,并求出当
的长,并求出当![]() 为何值时
为何值时![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解初一学生的体重情况,学校从体检结果中随机抽取了部分学生的体重数据并将抽样的数据进行了如下整理:
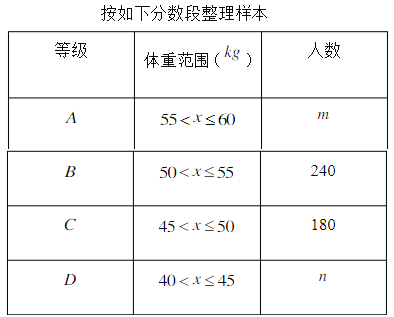
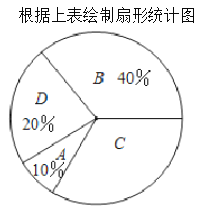
(1)请将图表中的数据补充完整;
(2)如果初一年级有1200名学生参加了本次体检,估计![]() 等级的人数;
等级的人数;
(3)请结合题目中的数据,给初一学生一个体检反馈或意见.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题是真命题的是( )
A.两直线平行,同位角相等
B.等边三角形是锐角三角形
C.如果两个实数是正数,那么它们的积是正数
D.全等三角形的对应角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
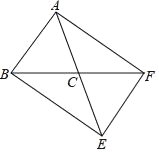
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
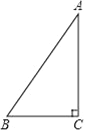
【题目】如图,在△ABC 中,∠C=90°
(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE
①求证:CD=DE;
②若sinA=![]() ,AC=6,求AD.
,AC=6,求AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com