
【题目】抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是第一象限内抛物线上一动点.
是第一象限内抛物线上一动点.
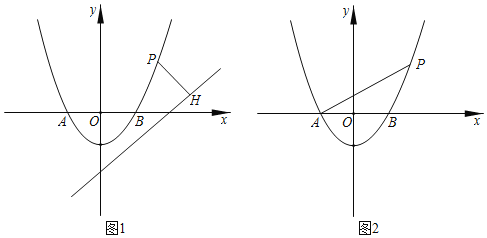
(1)直接写出抛物线的解析式;
(2)如图1,已知直线![]() 的解析式为
的解析式为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)如图2,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
科目:初中数学 来源: 题型:
【题目】某公司研发了一款成本为50元的新型玩具,投放市场进行试销售.其销售单价不低于成本,按照物价部门规定,销售利润率不高于90%,市场调研发现,在一段时间内,每天销售数量y(个)与销售单价x(元)符合一次函数关系,如图所示:
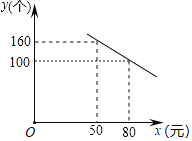
(1)根据图象,直接写出y与x的函数关系式;
(2)该公司要想每天获得3000元的销售利润,销售单价应定为多少元
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚准备进行如下操作试验:把一根长为80cm的铁丝剪成两段,并把每一段各围成一个正方形.要使这两个正方形的面积之和等于272cm2,小刚该怎么剪?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
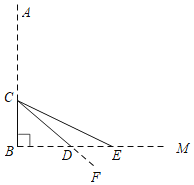
查看答案和解析>>
科目:初中数学 来源: 题型:
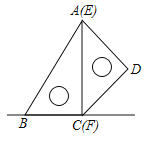
【题目】如图,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 拼合在一个平面上,边
拼合在一个平面上,边![]() 与
与![]() 重合,
重合,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿射线
出发沿射线![]() 方向滑动.当点
方向滑动.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,点
时,点![]() 运动的路径长为______
运动的路径长为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=![]() 时,求AD的长.
时,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣2x2﹣4x+6.
(1)用配方法求出函数的顶点坐标;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=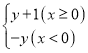 ,则称点Q为点P的“亲密点”.例如:点(1,2)的“亲密点”为点(1,3),点(﹣1,3)的“亲密点”为点(﹣1,﹣3).若点P在函数y=x2﹣2x﹣3的图象上,则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是( )
,则称点Q为点P的“亲密点”.例如:点(1,2)的“亲密点”为点(1,3),点(﹣1,3)的“亲密点”为点(﹣1,﹣3).若点P在函数y=x2﹣2x﹣3的图象上,则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是( )
A.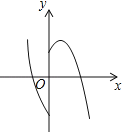 B.
B.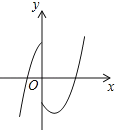
C.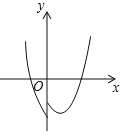 D.
D.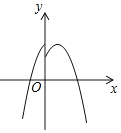
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com