
(本题12分)某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
(1)●操作发现:
在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是 ①②③④
(填序号即可)
①AF=AG= AB;②MD=ME;③整个图形是轴对称图形.
AB;②MD=ME;③整个图形是轴对称图形.
(2)●数学思考:
在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量和位置关系?请给出证明过程;
(3)●类比探究:
在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,则△MED的形状为__________ _________.等腰直角三角形
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年内蒙古满洲里市九年级4月月考数学试卷(解析版) 题型:选择题
如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值为( )

A. B.
B.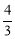 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期3月月考数学试卷(解析版) 题型:解答题
(本题8分)一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)从箱子中随机摸出两个球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省惠阳区三中初中毕业生学业综合测试数学试卷(解析版) 题型:解答题
如图,根据图中数据完成填空,再按要求答题:

sin2A1+sin2B1= ; sin2A2+sin2B2= ; sin2A3+sin2B3= .
(1)观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B= .
(2)如图④,在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,利用三角函数的定义和勾股定理,证明你的猜想.
(3)已知:∠A+∠B=90°,且sinA= ,求sinB.
,求sinB.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市番禺区综合测试(一模)数学试卷(解析版) 题型:选择题
据报道, 2014年6月,恒大集团与阿里巴巴集团实施战见解析合作,阿里巴巴注资12亿元入股广州恒大.将数据1200000000用科学记数法表示为( ).
(A)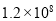 (B)
(B)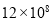 (C)
(C)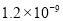 (D)
(D)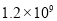
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com