Question

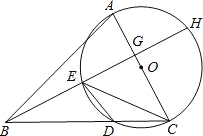
【题目】已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧上取一点E使∠EBC=∠DEC，延长BE依次交AC于点G，交⊙O于H．

（1）求证：AC⊥BH；

（2）若∠ABC=45°，⊙O的直径等于10，BD=8，求CE的长．

Answer 1

【答案】(1)证明见解析；（2）．

【解析】

试题分析：（1）连接AD，由圆周角定理即可得出∠DAC=∠DEC，∠ADC=90°，再根据直角三角形的性质即可得出结论；

（2）由∠BDA=180°-∠ADC=90°，∠ABC=45°可求出∠BAD=45°，利用勾股定理即可得出DC的长，进而求出BC的长，由已知的一对角线段和公共角，根据两对对应角相等的两三角形相似可得三角形BCE与三角形EDC相似，由相似得比例即可求出CE的长．

试题解析：（1）连接AD，

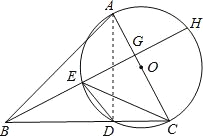
∵∠DAC=∠DEC，∠EBC=∠DEC，

∴∠DAC=∠EBC，

∵AC是⊙O的直径，

∴∠ADC=90°，

∴∠DCA+∠DAC=90°，

∴∠EBC+∠DCA=90°，

∴∠BGC=180°-（∠EBC+∠DCA）=180°-90°=90°，

∴AC⊥BH；

（2）∵∠BDA=180°-∠ADC=90°，∠ABC=45°，

∴∠BAD=45°，

∴BD=AD，

∵BD=8，∴AD=8，

在直角三角形ADC中，AD=8，AC=10，

根据勾股定理得：DC=6，则BC=BD+DC=14，

∵∠EBC=∠DEC，∠BCE=∠ECD，

∴△BCE∽△ECD，

∴，即CE2=BCCD=14×6=84，

∴CE==．