
����Ŀ���ڵ�����OAB�͵�����OCD�У�OA��OB��OC��OD������AC��BD���ڵ�M��

��1����ͼ1������AOB����COD��40����
��AC��BD��������ϵΪ�� ����
�ڡ�AMB�Ķ���Ϊ�� ����
��2����ͼ2������AOB����COD��90����
���ж�AC��BD֮�����������������ϵ����˵�����ɣ�
�����AMB�Ķ�����
��3���ڣ�2���������£�����CAB��30�����ҵ�C���M�غ�ʱ����ֱ��д��OD��OA֮����ڵ�������ϵ��
���𰸡���1����AC��BD����40������2����AC��BD�����ɼ���������90������3��OD��![]() OA��OD��
OA��OD��![]() OA
OA
��������
��1��֤����BOD�ա�AOC����AC=BD����OBD����OAC���������ڽǺͶ������AMB�Ķ�����
��2����ȣ�1��֤����BOD�ա�AOC����AC=BD����OBD����OAC���������ڽǺͶ������AMB�Ķ�����
��3������������֪D��B��C���㹲�ߣ��������������ͼ�Σ����ã�2���н��ۼ�����30������Ե�ֱ�DZߵ���б�ߵ�һ����ɶ�����AC��BC����AB��ʾ�������Ƴ�CD��AB�Ĺ�ϵ���ٸ���CD=![]() OD��AB=
OD��AB=![]() OA,���ɵó�OD��OA��������ϵ
OA,���ɵó�OD��OA��������ϵ
��1����ͼ1��ʾ��
�١ߡ�AOB����COD
���AOB+��AOD����COD+��AOD
���BOD����AOC
�ڡ�BOD�͡�AOC��

���BOD�ա�AOC��SAS��
��AC��BD.
�ʴ�Ϊ��AC��BD��
�ڡߡ�BOD�ա�AOC
���OBD����OAC
�ߡ�AOB��40����
���OAB+��OBA��180������AOB��180����40����140��
�֡ߡ�OAB+��OBA����OAB+��ABD+��OBD
���OAB+��OBA����OAB+��ABD+��OAC��140����
���MAB+��ABM��140��
���ڡ�ABM�У���AMB+��MAB+ABM��180����
���AMB��40��
�ʴ�Ϊ��40����
��2����ͼ2��ʾ��
��AC��BD��
�ߡ�AOB����COD��90����
���AOB+��AOD����COD+��AOD��
���BOD����AOC��
�ڡ�BOD�͡�AOC��
 ��
��
���BOD�ա�AOC��SAS��
��BD��AC
�ڡߡ�BOD�ա�AOC��
���OBD����OAC��
�֡ߡ�OAB+��OBA��90����
��ABO����ABM+��OBD��
��MAB����MAO+��OAB��
���MAB+��MBA��90����
�֡��ڡ�AMB�У���AMB+��ABM+��BAM��180����
���AMB��180��������ABM+��BAM����180����90����90����
��3����ͼ3��ʾ����AOB����COD��90����OA��OB��OC��OD����CAB��30����
���OAB����OBA����OCD����ODC��45����AB��![]() OA��CD��
OA��CD��![]() OC��
OC��
�ɣ�2���á�BOD�ա�AOC��SAS��
���ACO����BDO��45����BD��AC
���ACD����ACO+��OCD��90��
���ACB��90��
��BC��![]() AB
AB
�ɹ��ɶ����ã�AC��![]() ��
��![]() AB
AB
��CD��AC��BC��![]() AB
AB
��![]() OC��
OC��![]() ��
��![]() OA
OA
��OD��OC��![]() OA��
OA��
��ͼ4��ͬ���ɹ��ɶ����ã�AC��![]() ��
��![]() AB
AB
��CD��AC+BC��![]() AB
AB
��![]() OC��
OC��![]() ��
��![]() OA
OA
��OD��OC��![]() OA��
OA��
����������OD��![]() OA��OD��
OA��OD��![]() OA��
OA��






 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �ĶԽ����ཻ�ڵ�
�ĶԽ����ཻ�ڵ�![]() ��
��![]() ��
��![]() ��
��

![]() ��֤���ı���
��֤���ı���![]() �����Σ�
������
![]() ��
��![]() ������
������![]() �����Ϊ
�����Ϊ![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��֪����ͼ(1)����ƽ��ֱ������ϵ�У���![]() ��
��![]() ��
��![]() �ֱ����������ϣ���
�ֱ����������ϣ���![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �������
�������![]() �Ḻ������
�Ḻ������![]() ����λ����/����ٶ������˶�������
����λ����/����ٶ������˶�������![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �ϵ��е�.
�ϵ��е�.
(1)ֱ��д������![]() ___________��
___________��![]() ___________��
___________��![]() ___________.
___________.
(2)���![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() �룬�ʣ���
�룬�ʣ���![]() ��
��![]() ��ֱ�����ʱ�����ʱ
��ֱ�����ʱ�����ʱ![]() ��ֵ����˵������.
��ֵ����˵������.
(3)��ͼ(2)![]() ���ڵ�����������һ����
���ڵ�����������һ����![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() �ڵ����������˶�����
�ڵ����������˶�����![]() ���ж�
���ж�![]() �Ƿ�ƽ��
�Ƿ�ƽ��![]() ����˵������.
����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
�У�![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() ����
����![]() �ֱ�
�ֱ�![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ���е㣬��
���е㣬��![]() �������н��ۣ�
�������н��ۣ�![]() ��
��![]() ��
��![]() �ı���
�ı���![]() Ϊ���Σ�
Ϊ���Σ�![]() ��������ȷ�ĸ���Ϊ�� ��
��������ȷ�ĸ���Ϊ�� ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵȱ������Σ���D��E�ֱ���ֱ��BC��AC��.

(1)��ͼ1����BD=CEʱ������AD��BE���ڵ�P�����߶�AD��BE��������ϵ��____________;��APE�Ķ�����_______________��
(2)��ͼ2������BD=CE�����䣬AD��EB���ӳ��߽��ڵ�P����ô(1)�е����������Ƿ���Ȼ����?��˵������.
(3)��ͼ3����AE=BD������DE��AB�߽��ڵ�M����֤:��M��DE���е�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳��ֱ�Ϊ![]() ��
��![]() ������������
������������![]() ��
��![]() ���ŷ���һ������
���ŷ���һ������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]()
![]()

A. ![]() B. 2
B. 2![]() C. 2 D. 1
C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ܷ��ݳ�25�ף���ͼ��б����һ��ǽ�ϣ����ӵ���ǽ7�ף�
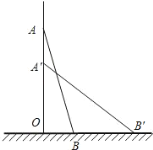
��1��������ӵĶ��˾�����ж�ߣ�
��2��������ӵĶ����»���4�ף���ô���ӵĵ���ˮƽ�����˼��ף�
��3�������ӵĶ����»��ľ��������ӵĵ�ˮƽ�����ľ������ʱ����ʱ���ӵĶ��˾�����ж�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��x�ύ�ڵ�A����ֱ��
��x�ύ�ڵ�A����ֱ��![]() ���ڵ�B��
���ڵ�B��
��1�����A��B��������ꣻ
��2��ֱ��д��y1��y2ʱx��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ���ֱ�
���ֱ�![]() ��
��![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��
��![]() ��
��![]() ��
��![]() ����֪�����ĸ�ʽ�ӣ���
����֪�����ĸ�ʽ�ӣ���![]() ����
����![]() ����
����![]() ����
����![]() .������ȷ��ʽ����__________����д��ţ�.
.������ȷ��ʽ����__________����д��ţ�.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com