
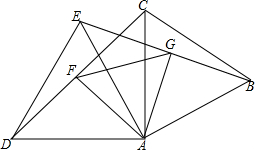
 如图,已知△ABC和△ADE均为等边三角形,连接CD、BE,作AF⊥CD于点F,AG⊥BE于点G,求证:△AFG为等边三角形.
如图,已知△ABC和△ADE均为等边三角形,连接CD、BE,作AF⊥CD于点F,AG⊥BE于点G,求证:△AFG为等边三角形.
|
|


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此,小明和小亮在课外活动中,报名参加了短跑训练小组,在近五次百米训练中,所测成绩如图所示,请根据图中的信息,解答下列问题.
短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此,小明和小亮在课外活动中,报名参加了短跑训练小组,在近五次百米训练中,所测成绩如图所示,请根据图中的信息,解答下列问题.| 平均数(秒) | 极差(秒) | 方差(秒2) | |
| 小明 | |||
| 小亮 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com