
【题目】如图,动点A在抛物线y=-x2+2x+3(0≤x≤3)上运动,直线l经过点(0,6),且与y轴垂直,过点A作AC⊥l于点C,以AC为对角线作矩形ABCD,则另一对角线BD的取值范围正确的是( )

A.2≤BD≤3B.3≤BD≤6C.1≤BD≤6D.2≤BD≤6
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)将两幅不完整的图补充完整;
(2)本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,二次函数y=mx 2 +2mx-4(m≠0)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
(1)求这个二次函数的解析式;
(2)点D的坐标为(-2,1),点P在二次函数的图象上,∠ADP为锐角,且tan∠ADP=2,求出点P的横坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:每个内角都相等的八边形叫做等角八边形.容易知道,等角八边形的内角都等于135°.下面,我们来研究它的一些性质与判定:
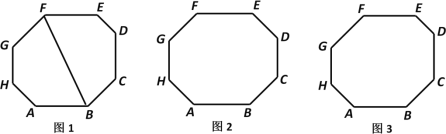
(1)如图1,等角八边形ABCDEFGH中,连结BF.
①请直接写出∠ABF+∠GFB的度数.
②求证:AB∥EF.
③我们把AB与EF称为八边形的一组正对边.由②同理可得:BC与FG,CD与GH,DE与HA这三组正对边也分别平行.请模仿平行四边形性质的学习经验,用一句话概括等角八边形的这一性质.
(2)如图2,等角八边形ABCDEFGH中,如果有AB=EF,BC=FG,则其余两组正对边CD与GH,DE与HA分别相等吗?证明你的结论.
(3)如图3,八边形ABCDEFGH中,若四组正对边分别平行,则显然有∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H.请探究:该八边形至少需要已知几个内角为135°,才能保证它一定是等角八边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
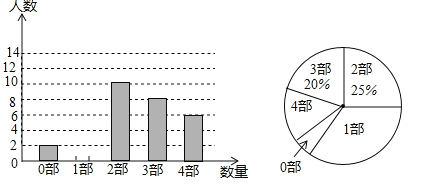
(1)本次调查所得数据的众数是 部,中位数是 部,扇形统计图中“1部”所在扇形的圆心角为 度.
(2)请将条形统计图补充完整;
(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
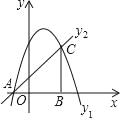
【题目】如图,抛物线y1=a(x﹣1)2+4与x轴交于A(﹣1,0).
(1)求该抛物线所表示的二次函数的表达式;
(2)一次函数y2=x+1的图象与抛物线相交于A,C两点,过点C作CB垂直于x轴于点B,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
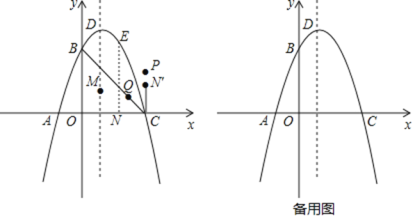
【题目】如图,在平面直角坐标系内,抛物线![]() 与x轴交于点A,C(点A在点C的左侧),与y轴交于点B,顶点为D.点Q为线段BC的三等分点(靠近点C).
与x轴交于点A,C(点A在点C的左侧),与y轴交于点B,顶点为D.点Q为线段BC的三等分点(靠近点C).
(1)点M为抛物线对称轴上一点,点E为对称轴右侧抛物线上的点且位于第一象限,当![]() 的周长最小时,求
的周长最小时,求![]() 面积的最大值;
面积的最大值;
(2)在(1)的条件下,当![]() 的面积最大时,过点E作
的面积最大时,过点E作![]() 轴,垂足为N,将线段CN绕点C顺时针旋转90°得到点N,再将点N向上平移
轴,垂足为N,将线段CN绕点C顺时针旋转90°得到点N,再将点N向上平移![]() 个单位长度.得到点P,点G在抛物线的对称轴上,请问在平面直角坐标系内是否存在一点H,使点D,P,G,H构成菱形.若存在,请直接写出点H的坐标,若不存在,请说明理由.
个单位长度.得到点P,点G在抛物线的对称轴上,请问在平面直角坐标系内是否存在一点H,使点D,P,G,H构成菱形.若存在,请直接写出点H的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某县美化城市工程招投标中,有甲、乙两个工程队投标经测算:甲队单独完成这项工程需要30天,若由甲队先做10天,剩下的工程由甲、乙合作12天可完成.问:
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需工程款2万元,该工程计划用时不超过35天,在不超过计划天数的前提下,由甲队先单独施工若干天,剩下的工程由乙队单独完成,那么安排甲队单独施工多少天工程款最省?最省的工程款是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com