
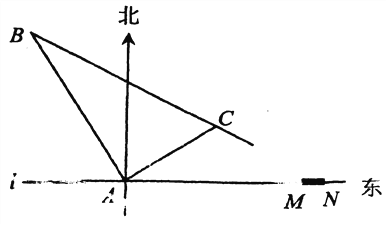
【题目】在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得二架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5万千米的C处.
⑴该飞机航行的速度是多少千米/小时?(结果保留根号)
⑵如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由。
【答案】⑴![]() km/h ⑵能降落在MN之间
km/h ⑵能降落在MN之间
【解析】试题分析:(1)先求出∠BAC=90°,然后利用勾股定理列式求解即可得到BC,再求解即可;
(2)作CE⊥l于E,设直线BC交l于F,然后求出CE、AE,然后求出AF的长,再进行判断即可.
试题解析:(1)由题意,得∠BAC=90°,
∴BC=![]() ,
,
∴飞机航行的速度为:10![]() ×60=600
×60=600![]() (km/h);
(km/h);
(2)能;
作CE⊥l于点E,设直线BC交l于点F.

在Rt△ABC中,AC=5![]() ,BC=10
,BC=10![]() ,
,
∴∠ABC=30°,即∠BCA=60°,
又∵∠CAE=30°,∠ACE=∠FCE=60°,
∴CE=ACsin∠CAE=![]() ,
,
AE=ACcos∠CAE=![]() .
.
则AF=2AE=15(km),
∴AN=AM+MN=14.5+1=15.5km,
∵AM<AF<AN,
∴飞机不改变航向继续航行,可以落在跑道MN之间.


科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
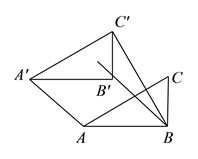
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.如图, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,将
,将![]() 沿
沿![]() 的平分线
的平分线![]() 方向平移得到
方向平移得到![]() ,连结
,连结![]() ,
, ![]() .
.
若平移后的四边形![]() 是“等邻边四边形”,求平移的距离(即线段
是“等邻边四边形”,求平移的距离(即线段![]() 的长).
的长).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com