
【题目】如图,A,B是反比例函数y=![]() 图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
图象上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=![]() OC,S四边形ABCD=9,则k值为( )
OC,S四边形ABCD=9,则k值为( )
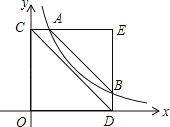
A.8B.10C.12D.16.
【答案】B
【解析】
分别延长CA、DB,它们相交于E,如图,设AC=t,则BD=t,OC=5t,根据反比例函数图象上点的坐标特征得到k=ODt=t5t,则OD=5t,所以B点坐标为(5t,t),于是AE=CE﹣CA=4t,BE=DE﹣BD=4t,再利用S四边形ABCD=S△ECD﹣S△EAB得到![]() 5t5t﹣
5t5t﹣![]() 4t4t=9,解得t2=2,然后根据k=t5t进行计算.
4t4t=9,解得t2=2,然后根据k=t5t进行计算.
解:分别延长CA、DB,它们相交于E,如图,
设AC=t,则BD=t,OC=5t,
∵A,B是反比例函数y=![]() 图象上两点,
图象上两点,
∴k=ODt=t5t,
∴OD=5t,
∴B点坐标为(5t,t),
∴AE=CE﹣CA=4t,BE=DE﹣BD=4t,
∵S四边形ABCD=S△ECD﹣S△EAB,
∴![]() 5t5t﹣
5t5t﹣![]() 4t4t=9,
4t4t=9,
∴t2=2,
∴k=t5t=5t2=5×2=10.
故选:B.


科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
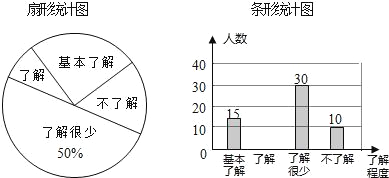
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 的图象与
的图象与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,且过点
,且过点![]() .
.
(1)求二次函数表达式;
(2)若点![]() 为抛物线上第一象限内的点,且
为抛物线上第一象限内的点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上(![]() 下方)是否存在点
下方)是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 到
到![]() 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
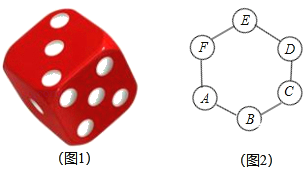
【题目】元旦期间,九年级某班六位同学进行跳圈游戏,具体过程如下:图1所示是一枚质地均匀的正方体骰子,骰子的六个面上的点数分别是1,2,3,4.5,6,如图2,正六边形ABCDEF的顶点处各有一个圈.跳圈游戏的规则为:游戏者每投掷一次骰子,假骰子向上的一面上的点数是几,就沿着正六边形的边逆时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就逆时针连续跳3个边长,落到圈D;若第二次掷得2.就从图D开始逆时针连续起跳2个边长,落到圈F…,设游戏者从圈A起跳
(1)小明随机掷一次骰子,求落回到圈A的概率P1;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率P2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
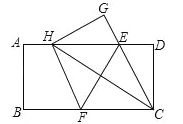
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2![]() .
.
以上结论中,你认为正确的有 .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
材料1 若一元二次方程ax2+bx+c=0(a≠0)的两个根为x1,x2则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
材料2 已知实数m,n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,求![]() 的值.
的值.
解:由题知m,n是方程x2﹣x﹣1=0的两个不相等的实数根,根据材料1得m+n=1,mn=﹣1,所以![]() =﹣3.
=﹣3.
根据上述材料解决以下问题:
(1)材料理解:一元二次方程5x2+10x﹣1=0的两个根为x1,x2,则x1+x2= ,x1x2= .
(2)类比探究:已知实数m,n满足7m2﹣7m﹣1=0,7n2﹣7n﹣1=0,且m≠n,求m2n+mn2的值:
(3)思维拓展:已知实数s、t分别满足19s2+99s+1=0,t2+99t+19=0,且st≠1.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
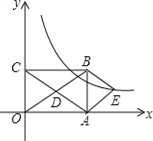
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com