
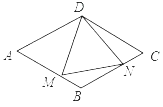
【题目】如图,在边长为4的菱形ABCD中,∠A=60°,点M、N是边AB、BC上的动点,若△DMN为等边三角形,点M、N不与点A、B、C重合,则△BMN面积的最大值是_____.
【答案】![]()
【解析】
先判断出△DMB≌△DNC,进而判断出当△DMN的面积最小时,△BMN的面积最大,即可得出结论.
解:连接BD,
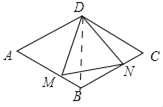
∵四边形ABCD是菱形,
∴BD=CD,DN=DM,
∵∠BDM=∠MDN﹣∠BDN,
∵∠CDN=∠BDC﹣∠BDN,∠MDN=∠BDC=60°,
∴∠CDN=∠BDM,
∴△DMB≌△DNC(SAS),
∴S△DMB=S△DNC,
∴S四边形DMBN=S△DBC![]() ,
,
∵S△BMN=S四边形DMBN﹣S△DMN,
∴当△DMN的面积最小时,△BMN的面积最大,
当DN⊥BC时,△DMN的边长最短,
即:△DMN的面积最小,此时DN=![]() ,
,
即:S△DMN=![]() ,
,
∴△BMN的面积的最大值为![]() ,
,
故答案为:![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】为更好的了解中学生课外阅读的情况,学校团委将初一年级学生一学期阅读课外书籍量分为A(3本以内)、B(3——6本)、C(6——10本)、D(10本以上)四种情况进行了随机调查,并根据调查结果制成了如下两幅不完整的统计图.请结合统计图所给信息解答上列问题:
(1)在扇形统计图中C所占的百分比是多少?
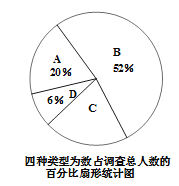
(2)请将折线统计图补充完整;

(3)学校团委欲从课外阅读量在10本以上的同学中随机邀请两位参加学校举办的“书香致远 墨卷至恒”主题读书日的形象大使,请你用列表法或画树状图的方法,求所选出的两位同学恰好都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
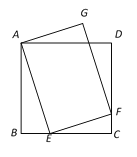
【题目】如图,已知正方形ABCD中,点E是BC上的一个动点,EF⊥AE交CD于点F,以AE,EF为边作矩形AEFG,若AB=4,则点G到AD距离的最大值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备购进一批产品进行销售,该产品的进货单价为6元/个.根据市场调查,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.关于日销售量y(个)与销售单价x(元/个)的几组数据如表:
x | 10 | 12 | 14 | 16 |
y | 300 | 240 | 180 | m |
(1)求出y与x之间的函数关系式(不要求写出自变量的取值范围)及m的值.
(2)按照(1)中的销售规律,当销售单价定为17.5元/个时,日销售量为 个,此时,获得日销售利润是 .
(3)为防范风险,该公司将日进货成本控制在900(含900元)以内,按照(1)中的销售规律,要使日销售利润最大,则销售单价应定为多少?并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+b经过C(﹣2,4),D(﹣4,4)两点.
(1)求抛物线y1的函数表达式;
(2)将抛物线y1沿x轴翻折,再向右平移,得到抛物线y2,与y2轴交于点F,点E为抛物线2上一点,要使以CD为边,C、D、E、F四点为顶点的四边形为平行四边形,求所有满足条件的抛物线y2的函表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB= ![]() ,BC=1,连结BF,分别交AC、DC、DE于点P、Q、R.
,BC=1,连结BF,分别交AC、DC、DE于点P、Q、R.
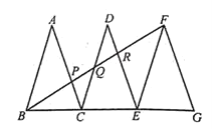
(1)求证:△BFG∽△FEG
(2)求sin∠FBG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A![]() 的直线l分别与x轴、y轴交于点C,D.
的直线l分别与x轴、y轴交于点C,D.
(1)求直线l的函数表达式.
(2)P为x轴上一点,若△PCD为等腰三角形直接写出点P的坐标.
(3)将线段AB绕B点旋转90°,直接写出点A对应的点A的坐标.
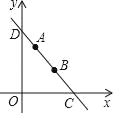
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量建筑物AC的高度,从距离建筑物底部C处50米的点D(点D与建筑物底部C在同一水平面上)出发,沿坡度i=1:2的斜坡DB前进10![]() 米到达点B,在点B处测得建筑物顶部A的仰角为53°,求建筑物AC的高度.(结果精确到0.1米.参考数据:sin53°≈0.798,cos53°≈0.602,tan53°≈1.327.)
米到达点B,在点B处测得建筑物顶部A的仰角为53°,求建筑物AC的高度.(结果精确到0.1米.参考数据:sin53°≈0.798,cos53°≈0.602,tan53°≈1.327.)
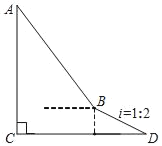
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com