
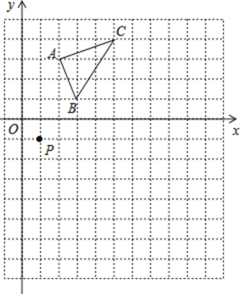
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() .
.
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)以点![]() 为位似中心,在如图所示的网格中画出
为位似中心,在如图所示的网格中画出![]() 的位似图形
的位似图形![]() ,使
,使![]() 与
与 ![]() 的相似比为
的相似比为![]() ;
;
(3)点![]() 的坐标是 .
的坐标是 .
【答案】(1)详见解析;(2)详见解析;(3)点![]() 的坐标是
的坐标是![]()
【解析】
(1)根据关于x轴对称性质找到A1、B1、C1的位置,然后画出图形即可;
(2)分别连接A1、B1、C1和P,然后延长扩大2倍,分别得到A2、B2、C2的位置,再画出图形即可;
(3)先根据轴对称的性质求出C1的坐标,再由位似的知识算出C2的坐标即可.
解: (1) 根据关于x轴对称性质找到A1、B1、C1的位置,然后画出图形,如图所示:
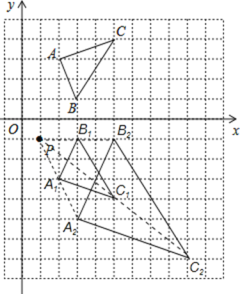
(2) 分别连接A1、B1、C1和P,然后延长扩大2倍,分别得到A2、B2、C2的位置,再画出图形,如图所示:
(3) 根据轴对称的性质知C1的坐标(5,-4),再以点![]() 为位似中心,相似比为
为位似中心,相似比为![]() ,则点
,则点![]() 的坐标是
的坐标是![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】D为等腰Rt△ABC斜边AB的中点,DM⊥DN,DM,DN分别交BC,CA于点E,F.
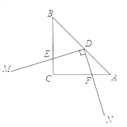
(1)当∠MDN绕点D转动时,求证:DE=DF.
(2)若AB=2,求四边形DECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
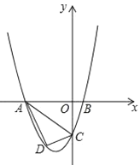
【题目】已知,如图抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.B的坐标为(1,0),且OC=4OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.B的坐标为(1,0),且OC=4OB.
(1)求点C坐标及抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求△ACD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,进价为每件15元,规定每件商品售价不低于进价,且每天销售量不低于90件经调查发现,每天的销售量y(件)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:
每个商品的售价x(元) | … | 30 | 40 | 50 | … |
每天的销售量y(件) | … | 100 | 80 | 60 | … |
(1)填空:y与x之间的函数关系式是______.
(2)设商场每天获得的总利润为w(元),求w与x之间的函数关系式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2﹣4amx+3am2(a、m为参数,且a>0,m>0)与x轴交于A、B两点(A在B的左边),与y轴交于点C.
(1)求点B的坐标(结果可以含参数m);
(2)连接CA、CB,若C(0,3m),求tan∠ACB的值;
(3)如图②,在(2)的条件下,抛物线的对称轴为直线l:x=2,点P是抛物线上的一个动点,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的的等腰直角三角形.若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
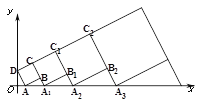
【题目】在平面直角坐标系![]() 中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为____________;第n个正方形的面积为____________.
中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为____________;第n个正方形的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
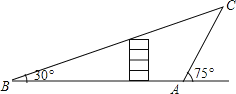
【题目】.如图,小明在大楼的东侧A处发现正前方仰角为75°的方向上有一热气球在C处,此时,小亮在大楼的西侧B处也测得气球在其正前方仰角为30°的位置上,已知AB的距离为60米,试求此时小明、小亮两人与气球的距离AC和BC.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
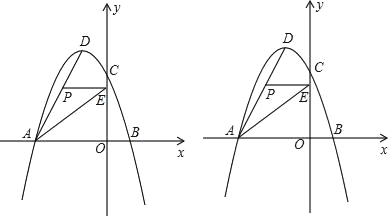
查看答案和解析>>
科目:初中数学 来源: 题型:
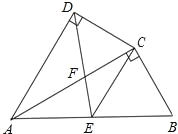
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com