
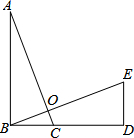
 如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°.
如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$$>\frac{a+b}{a+b+c}$ | B. | $\frac{a}{b}$$<\frac{a+b}{a+b+c}$ | C. | $\frac{a}{b}$=$\frac{a+b}{a+b+c}$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进、出水管.在打开进水管到关停进、出水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示
一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进、出水管.在打开进水管到关停进、出水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
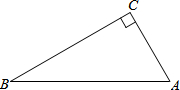 如图,在△ABC中,∠C=90°,∠A>∠B.
如图,在△ABC中,∠C=90°,∠A>∠B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
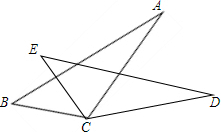 如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )| A. | AB=DE | B. | ∠B=∠E | C. | AC=DC | D. | ∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com