Question

20．已知：如图1，二次函数y=ax²-2ax+c（a＞0）的图象与y轴交于点C（0，-4），与x轴交于点A、B两点，点A的坐标为（4，0）．
（1）求该抛物线的函数解析式；
（2）点P（t，0）是线段OB上一动点（不与O、B重合），点E是线段BC上的点，以点B、P、E为顶点的三角形与三角形ABC相似，连结CP，求△CPE的面积S与t的函数关系式；
（3）如图2，若平行于x轴的动直线与该抛物线交于点Q，与直线AC交于点F，点D的坐标为（2，0），则存在这样的直线，使得△ODF为等腰三角形，请直接写出点Q坐标．

Answer 1

分析 （1）根据待定系数法，可得函数解析式；
（2）可先设P的坐标为（m，0）；根据相似三角形的性质，可得S_△BEP，根据S_△CPE=S_△BOC-S_△BPE-S_OPC，可得函数关系式；
（3）本题要分三种情况进行求解：①当OD=OF时，根据等腰直角三角形，可得出F的坐标应该是（2，2），根据F的纵坐标代入抛物线的解析式中即可求出Q的坐标；②当OF=DF时，根据线段垂直平分线的性质，可得OM=1，根据等腰直角三角形的性质，可得FM=AM=3，也就得出了F的纵坐标，根据①的方法求出Q的坐标；③当OD=OF时，OF=2，由于O到AC的最短距离为2$\sqrt{2}$，因此此种情况是不成立的，综合上面的情况即可得出符合条件的P的坐标

解答 解：（1）把C（0，-4）和A（4，0）代入y=ax²-2ax+c（a＞0）得，
$\left\{\begin{array}{l}{16a-8a+c=0}\\{c=-4}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-4}\end{array}\right.$
解析式为y=$\frac{1}{2}$x²-x-4；
（2）BP=t+2，OP=-t，S_△ABC=4×6÷2=12，S_△OPC=4×（-t）÷2=2t，
①△BPE∽△BAC，则$\frac{BP}{AB}$=$\frac{2+t}{6}$，
则$\frac{{S}_{△BPE}}{{S}_{△ABC}}$=（$\frac{t+2}{6}$）²，S_△BPE=（$\frac{t+2}{6}$）²×12=$\frac{（t+2）^{2}}{3}$
S_△CPE=S_△BOC-S_△BPE-S_OPC=4-$\frac{（t+2）^{2}}{3}$-（-2t）=-$\frac{1}{3}$t²+$\frac{2}{3}$t+$\frac{8}{3}$
②△BEP∽△BAC，则$\frac{BP}{BC}$=$\frac{t+2}{\sqrt{20}}$，
则$\frac{{S}_{△BEP}}{{S}_{ABC}}$=（$\frac{t+2}{\sqrt{20}}$）²，S_△BEP=（$\frac{t+2}{\sqrt{20}}$）²×12=$\frac{3（t+2）^{2}}{5}$
S_△CPE=S_△BOC-S_△BPE-S_OPC=4-$\frac{3（t+2）^{2}}{5}$-（-2t）=-$\frac{3}{5}$t²-$\frac{2}{5}$t+$\frac{8}{5}$   
（3）存在这样的直线，使得△ODF是等腰三角形，理由为：
在△ODF中，分三种情况考虑：
①若DO=DF，如图1：，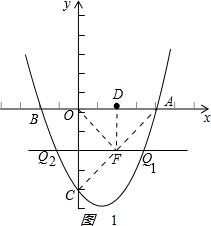
∵A（4，0），D（2，0），
∴AD=OD=DF=2，
又在Rt△AOC中，OA=OC=4，
∴∠OAC=45°，
∴∠DFA=∠OAC=45°，
∴∠ADF=90°，
此时，点F的坐标为（2，-2），
由$\frac{1}{2}$x²-x-4=-2，
解得：x₁=1+$\sqrt{5}$，x₂=1-$\sqrt{5}$，
此时，点P的坐标为：P（1+$\sqrt{5}$，-2）或P（1-$\sqrt{5}$，-2）；
②若FO=FD，过点F作FM⊥x轴于点M，如图2：，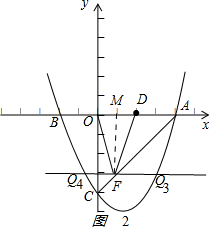
由等腰三角形的性质得：OM=$\frac{1}{2}$OD=1，
∴AM=3，
∴在等腰直角△AMF中，MF=AM=3，
∴F（1，3），
由$\frac{1}{2}$x²-x-4=-3，
解得：x₁=1+$\sqrt{3}$，x₂=1-$\sqrt{3}$，
此时，点P的坐标为：P（1+$\sqrt{3}$，-3）或P（1-$\sqrt{3}$，-3）；
③若OD=OF，
∵OA=OC=4，且∠AOC=90°，
∴AC=4 $\sqrt{2}$，
∴点O到AC的距离为2√2，而OF=OD=2＜2√2，与OF≥2√2矛盾，
所以AC上不存在点使得OF=OD=2，
此时，不存在这样的直线l，使得△ODF是等腰三角形；
综上所述，存在这样的直线l，使得△ODF是等腰三角形，点Q的坐标为：Q₁（1+$\sqrt{5}$，-2）或Q₂（1-$\sqrt{5}$，-2）或Q₃（1+$\sqrt{3}$，-3）或Q₄（1-$\sqrt{3}$，-3）．

点评 本题考查了二次函数的综合题，利用待定系数法二次函数解析式；利用三角形相似的判定与性质得出S_△BPE是解题关键，又利用了面积的和差求函数关系式；要注意的是（3）中不确定等腰三角形的腰是哪些线段时，要分类进行讨论．