
分析 (1)观察给定等式,发现两分数的分子之和为8,根据规律猜想出结论;
(2)将等式的左边通分、合并同类项,得出结果后与等式的右边进行比较,从而得出结论.
解答 (1)解:观察上面等式发现等式左边两分数的分子相加为8,且分子与分母中前面的数相等,
故猜想存在$\frac{a}{a-4}+\frac{8-a}{8-a-4}$=$\frac{a}{a-4}+\frac{8-a}{4-a}$=2(a≠4).
(2)证明:等式左边=$\frac{a}{a-4}+\frac{8-a}{4-a}$,
=$\frac{a-(8-a)}{a-4}$,
=$\frac{2(a-4)}{a-4}$,
=2=右边.
故该结论正确.
点评 本题考查了数字的变化以及分解因式,解题的关键:(1)发现等式前面两分数分子相加为定值8;(2)利用分解因式的方法证明结论.本题属于中档题,有点难度,难点在于规律的发现,解决该题型题目时,根据给定算式找出规律是关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
 △ABC在直角坐标系中的位置如图所示,若将△ABC绕点O旋转,点C的对应点为点D,其中A(1,2),B(-1,0),C(3,-1),D(-1,-3),则旋转后点A的对应点E的坐标为( )
△ABC在直角坐标系中的位置如图所示,若将△ABC绕点O旋转,点C的对应点为点D,其中A(1,2),B(-1,0),C(3,-1),D(-1,-3),则旋转后点A的对应点E的坐标为( )| A. | (-1,2) | B. | (0,-1) | C. | (1,-3) | D. | (2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 步行人数为30人 | B. | 骑车人数占总人数的10% | ||
| C. | 该班总人数为50人 | D. | 乘车人数是骑车人数的40% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
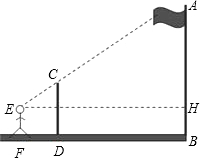 九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,则旗杆AB的高度13.5m.
九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图所示,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,则旗杆AB的高度13.5m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-y)2=(y-x)2 | B. | (x+6)(x-6)=x2-6 | ||
| C. | (x+y)=x2+y2 | D. | (3x-y)(-3x+y)=9x2-y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com