
���� ��1���������A��B�����꣬�������ô���ϵ�����������ֱ��CD�Ľ���ʽ��Ȼ�����AC��BC����ֱ��AC��ֱ��BC�Ľ���ʽ��һ���������Ϊ�������������C�����꣬�Ӷ����ô���ϵ�������k��ֵ��
��2�����ݵ���ֱ�������ε����ʣ����D������꣬�ٸ�����ֱ�ߴ�ֱ�õ�CD��б�ʣ��Ӷ����CD�Ľ���ʽ���ٽⷽ��������������꣬�õ�M������ꣻ
��3���ӳ�BQ��y�����C���ı���ABQPΪ�������Σ����ԡ�PAB=��QBA������CA=CB�������C�����꣬����CA=CB���з��������C�������꣬�ٰѵ�B��������룬�����BQ�Ľ���ʽ��
��� 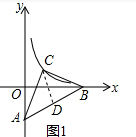 �⣺��ͼ1 ��y=$\frac{1}{2}$x+1�У���x=0����ã�y=-2����A�������ǣ�0��-2����
�⣺��ͼ1 ��y=$\frac{1}{2}$x+1�У���x=0����ã�y=-2����A�������ǣ�0��-2����
��y=0����ã�x=4����B�������ǣ�4��0����
��AB���е�ΪD������CD��
��D�������ǣ�2��-1����
�ߡ�ACB����ABΪ�ĵ���ֱ�������Σ�
��CD��AB��AB=2$\sqrt{5}$��AC=BC=$\sqrt{10}$
��ֱ��CD�Ľ���ʽ��y=-2x+b��
����D�������ǣ�2��-1����
��b=3��
��CD�Ľ���ʽ��y=-2x+3��
��C��x��-2x+3����
��${x}^{2}{+��-2x+3+2��}^{2}{=��\sqrt{10}��}^{2}$��
���x1=1��x2=3������������ȥ����
��C��1��1����
�跴���������Ľ���ʽ��y=$\frac{k}{x}$������C��1��1����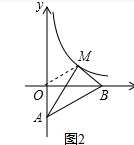
��k=1��
�෴���������Ľ���ʽ��y=$\frac{1}{x}$��
��2���ߵ�MΪ����������y=$\frac{k}{x}$��ͼ��һ���ޣ���һ�㣬��S��MAB=S��OAB��
��ֱ��OM��AB����ֱ��OM�Ľ���ʽΪy=$\frac{1}{2}$x��
��ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=\frac{1}{x}}\end{array}\right.$�ã�$\left\{\begin{array}{l}{{x}_{1}=\sqrt{2}}\\{{y}_{1}=\frac{\sqrt{2}}{2}}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-\sqrt{2}}\\{{y}_{2}=-\frac{\sqrt{2}}{2}}\end{array}\right.$������������ȥ����
��M��$\sqrt{2}$��$\frac{\sqrt{2}}{2}$����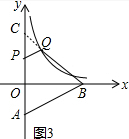
��3����ͼ3���ӳ�BQ��y�����C��
���ı���ABQPΪ�������Σ�
���PAB=��QBA��
��CA=CB��
��ֱ��BQ�Ľ���ʽΪy=kx+b��
��C��0��b����
�ࣨb+2��2=b2+42��
��b=6��
��b=6��B��4��0������y=kx+b��
��k=-$\frac{3}{2}$��
��ֱ��BQ�Ľ���ʽΪ��y=-$\frac{3}{2}$x+3��
���� �����ۺϿ����˷�����������һ�κ����Ľ���ʽ����Ӧ�������������ȵ���ͬ���õ�����ȣ�����ֱ�������ε����ʣ��������εȶ��֪ʶ�㣮�����Ѷ��Դ��ۺ��ԱȽ�ǿ��ע��Ը���֪ʶ������Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
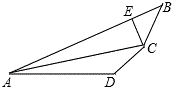 ��ͼ��ACƽ�֡�BAD��CE��AB����2AE=AB+AD����̽����ADC���ABC�Ĺ�ϵ��
��ͼ��ACƽ�֡�BAD��CE��AB����2AE=AB+AD����̽����ADC���ABC�Ĺ�ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | �� | -1 | 0 | 1 | 2 | �� |
| y | �� | -3 | 1 | 3 | 1 | �� |
| A�� | �����߿������� | B�� | ��������y�ύ�ڸ����� | ||
| C�� | ��x=3ʱ��y��0 | D�� | ����ax2+bx+c=0��������2��3֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
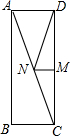 ��ͼ���ھ���ABCD�У�AD=3��AB=9��M��DC��һ�㣬DM=4��N��AC�ϵ�һ�����㣬���DMN���ܳ�����Сֵ��$\sqrt{34}$+4��
��ͼ���ھ���ABCD�У�AD=3��AB=9��M��DC��һ�㣬DM=4��N��AC�ϵ�һ�����㣬���DMN���ܳ�����Сֵ��$\sqrt{34}$+4���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com