
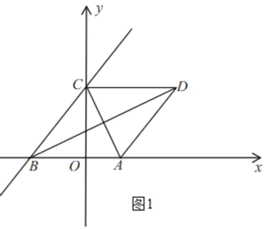
【题目】如图,在平面直角坐标系中,一次函数y=![]() x+4的图象与x轴交于点B,与y轴交于点C,二次函数y=
x+4的图象与x轴交于点B,与y轴交于点C,二次函数y=![]() x2+bx+c的图象经过点A(2,0)和点C,抛物线与x轴交于点A和点E(点A在点E的左侧),连接AC,将△ABC沿AC折叠,得到点B的对应点为点D.
x2+bx+c的图象经过点A(2,0)和点C,抛物线与x轴交于点A和点E(点A在点E的左侧),连接AC,将△ABC沿AC折叠,得到点B的对应点为点D.
(1)求二次函数的表达式;
(2)求点D坐标,并判定点D是否在该二次函数的图象上;
(3)①在线段AC上找一点F,使得△OBF的周长最小,直接写出此时点F的坐标.②在①的基础上,过点F的一条直线与抛物线对称轴右侧部分交于点N,交线段AD于点M,连接NA、ND,使△AMF与△AMN的面积比为4:1,请直接写出△AND的面积.
【答案】(1)![]() ;(2)D(5,4),点D是否在该二次函数的图象上;(3)①F
;(2)D(5,4),点D是否在该二次函数的图象上;(3)①F![]() ;②△AND的面积为
;②△AND的面积为![]() .
.
【解析】
(1)先根据一次函数的解析式求出点C坐标,再利用待定系数法即可得;
(2)先根据一次函数的解析式求出点B坐标,再根据点![]() 坐标可得
坐标可得![]() ,再根据旋转的性质、菱形的判定与性质可得CD∥AB,CD=AB=5,从而可得点D坐标,然后根据二次函数的解析式即可得出答案;
,再根据旋转的性质、菱形的判定与性质可得CD∥AB,CD=AB=5,从而可得点D坐标,然后根据二次函数的解析式即可得出答案;
(3)①先由题(2)的结论得出点B、D关于AC对称,再根据轴对称的性质、两点之间线段最短得出,![]() 的周长最小时,点F的位置,然后利用待定系数法求出AC、OD的解析式,联立求解即可得点F坐标;
的周长最小时,点F的位置,然后利用待定系数法求出AC、OD的解析式,联立求解即可得点F坐标;
②先根据“△AMF与△AMN的面积比为4:1”求出FM=4MN,再利用待定系数法求出AD的解析式,从而可得![]() 的长,然后根据相似三角形的判定与性质可得NH的长,最后利用点A、D坐标和三角形的面积公式即可得.
的长,然后根据相似三角形的判定与性质可得NH的长,最后利用点A、D坐标和三角形的面积公式即可得.
(1)∵一次函数![]() 的图象与y轴交于点C
的图象与y轴交于点C
∴![]()
∵点![]() 在二次函数
在二次函数![]() 的图象上
的图象上
∴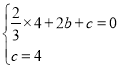 ,解得
,解得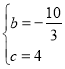
故二次函数的解析式为![]() ;
;
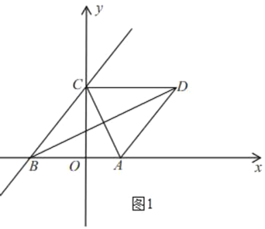
(2)如图1,对于一次函数![]()
令y=0,则![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴BC=AB
由折叠的性质可知,BC=CD,AB=AD
∴AB=AD=CD=BC
∴四边形ABCD是菱形
∴CD∥AB,CD=AB=5
∴点D横坐标为5,纵坐标与点C纵坐标相等
![]()
由(1)知,二次函数的解析式为![]()
当x=5时,![]()
∴点D在二次函数![]() 的图象上
的图象上
故点D坐标为![]() ,且在二次函数
,且在二次函数![]() 的图象上;
的图象上;
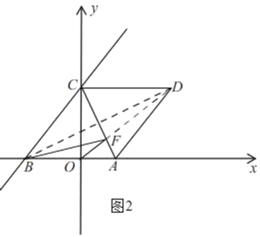
(3)①如图2,连接FD、BD
由(2)知,四边形ABCD是菱形
∴点B关于AC的对称点为D
![]()
![]() 的周长为
的周长为![]()
由两点之间线段最短得,当点![]() 在一条线上时,
在一条线上时,![]() 的周长最小
的周长最小
![]()
∴直线OD的解析式为![]()
![]()
∴直线AC的解析式为![]()
联立OD、AC的函数解析式得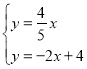
解得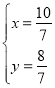
∴![]() ;
;
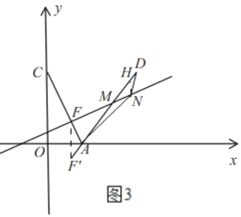
②如图3,由①知,![]()
∵△AMF与△AMN的面积比为![]()
∴FM=4MN
∵![]()
∴直线AD的解析式为![]()
过点F作![]() 轴,交DA的延长线于点
轴,交DA的延长线于点![]()
将![]() 代入
代入![]() 得,
得,![]()
∴![]()
![]()
过点N作NH∥y轴,交AD于H
∴![]()
∴![]()
∴![]()
∴![]()
设点A横坐标为![]() ,点D横坐标为
,点D横坐标为![]()
∴![]()
故△AND的面积为![]() .
.


科目:初中数学 来源: 题型:
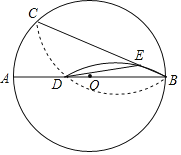
【题目】如图,将⊙O上的![]() 沿弦BC翻折交半径OA于点D,再将
沿弦BC翻折交半径OA于点D,再将![]() 沿BD翻折交BC于点E,连结DE.若AB=10,OD=1,则线段DE的长为( )
沿BD翻折交BC于点E,连结DE.若AB=10,OD=1,则线段DE的长为( )
A.5B.2![]() C.2
C.2![]() D.
D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 、
、![]() 是圆
是圆![]() 中的两条弦,连接
中的两条弦,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() .
.
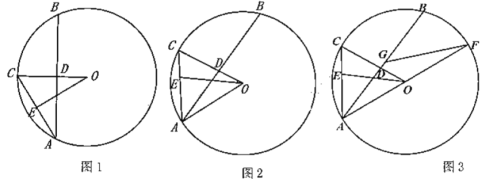
(1)如图1,若![]() ,求证:弧
,求证:弧![]()
![]() 弧
弧![]() ;
;
(2)如图2,连接![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在第(2)问的条件下,延长![]() 交圆
交圆![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,若
,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
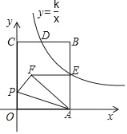
【题目】如图,将矩形OABC置于一平面直角坐标系中,顶点A,C分别位于x轴,y轴的正半轴上,点B的坐标为(5,6),双曲线y=![]() (k≠0)在第一象限中的图象经过BC的中点D,与AB交于点E,P为y轴正半轴上一动点,把△OAP沿直线AP翻折,使点O落在点F处,连接FE,若FE∥x轴,则点P的坐标为___.
(k≠0)在第一象限中的图象经过BC的中点D,与AB交于点E,P为y轴正半轴上一动点,把△OAP沿直线AP翻折,使点O落在点F处,连接FE,若FE∥x轴,则点P的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
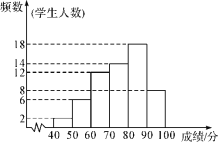
【题目】为了解某中学去年中招体育考试中女生”一分钟跳绳”项目的成绩情况,从中抽取部分女生的成绩,绘制出如图所示的频数分布直方图(从左到右依次为第一组到第六组,每小组含最小值,不含最大值)和扇形统计图,请根据下列统计图中提供的信息解决下列问题

(1)本次抽取的女生总人数为 第六小组人数占总人数的百分比为 请补全频数分布直方图;
(2)题中样本数据的中位数落在第 组内;
(3)若“一分钟跳绳”不低于130次的成绩为优秀,这个学校九年级共有女生560人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有300名学生,为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,将他们的成绩进行整理、描述和分析.下面给出了部分信息:
Ⅰ.A课程成绩的频数分布直方图如下(数据分成6组):
Ⅱ.A课程成绩在70≤x<80这一组的是:70, 71, 71,71,76,76,77,78,78, 78.5,78.5,79, 79, 79.5.
Ⅲ.A,B两门课程成绩的中位数、众数、平均数如下表所示:
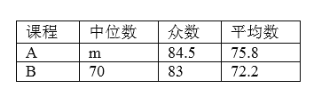
根据以上信息,回答下列问题:
(1)写出表中m的值,m=________;
(2)在此次测试中,某学生的A课程成绩为78分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”)
(3)假设该年级学生都参加此次测试,估计A课程成绩超过该课程平均分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,连接在一起的两个等边三角形的边长都为2cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2018cm后,它停在了点_____上.
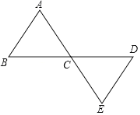
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国流传了上千年的传统节日,全国各地举行了丰富多彩的纪念活动,为了继承传统,减缓学生考前的心理压力,某班学生组织了一次拔河比赛,裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置,规则是:石头胜剪刀,剪刀胜布,布胜石头,手势相同则再决胜负.
(1)用列表或画树状图法,列出甲、乙两队手势可能出现的情况;
(2)裁判员的这种做法对甲、乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
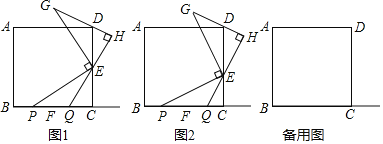
【题目】综合与实践
如图,点![]() 是正方形
是正方形![]() 的边
的边![]() 上一点,点
上一点,点![]() 在线段
在线段![]() 上,将线段
上,将线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
探究发现
(1)如图1,若点![]() 是线段
是线段![]() 的中点,直接写出线段
的中点,直接写出线段![]() 的数量关系为______;
的数量关系为______;
(2)如图2,若点![]() 不是线段
不是线段![]() 的中点,线段
的中点,线段![]() 的数量关系为______,填写出证明过程;
的数量关系为______,填写出证明过程;
(3)当![]() ,
,![]() 时,连接
时,连接![]() ,则
,则![]() ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com