
【题目】已知,如图,在边长为10的菱形ABCD中,cos∠B=![]() ,点E为BC边上的中点,点F为边AB边上一点,连接EF,过点B作EF的对称点B′,
,点E为BC边上的中点,点F为边AB边上一点,连接EF,过点B作EF的对称点B′,
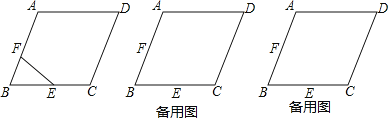
(1)在图(1)中,用无刻度的直尺和圆规作出点B′(不写作法,保留痕迹);
(2)当△EFB′为等腰三角形时,求折痕EF的长度.
(3)当B′落在AD边的中垂线上时,求BF的长度.
【答案】(1)尺规作图见解析;(2)EF=5或![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)分别以F、E为圆心,FB、EB为半径画弧,两弧交于点B,B即为所求;
(2)分情况①当BE=EF时,②BE=BF时,③EF=BF时讨论即可;
(3)连接BB,FE,可知BB⊥FE,依据翻折及勾股定理即可解得.
试题解析:(1)尺规作图:
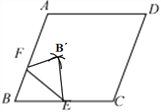
(2)由翻折知:△FBE≌△FBE,
∴BE=BE,BF=BF,
∵点E为BC边上的中点,
∴BE=BE=5,
① 当BE=EF时,EF=5,
②当BE=BF时,过点F作FG⊥BE于点G,
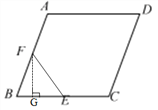
在Rt△FBG中,BE=BF=5,cos∠B=![]() ,
,
∴BG=![]() ,GE=BE-BG=
,GE=BE-BG=![]() ,
,
FG=![]() ,
,
在Rt△FEG中,FE=![]() ;
;
③当EF=BF时,
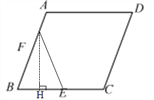
过点F作FH⊥BE于点H,BH=![]() BE=
BE=![]() ,
,
在Rt△FBH中, cos∠B=![]() ,
,
∴BF=BH×![]() =
=![]() ,
,
∴EF=![]() ,
,
综上:EF=5或![]() 或
或![]() .
.
(3)
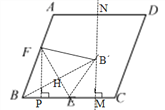
如图:连接BB,FE,交点 为H,
则BB⊥FE,
∵AN=DN=BE=CE=5,
∴BM=4,MN=![]() ,B B=
,B B=![]() ,
,
BH=![]() ,
,
∴BF=BF=![]() .
.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
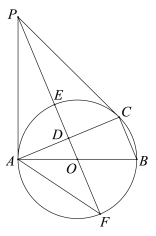
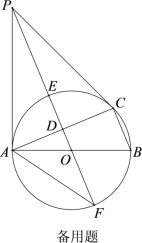
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
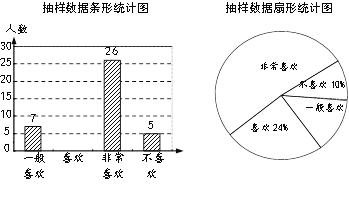
【题目】某校用随机抽样的方法在九年级开展了“你是否喜欢网课”的调查,并将得到的数据整理成了以下统计图(不完整).
(1)此次共调查了 名学生;
(2)请将条形统计图补充完整;
(3)若该学校九年级共有300名学生,请你估计其中“非常喜欢”网课的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
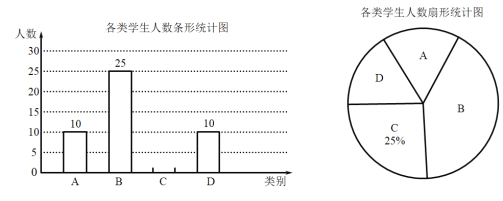
【题目】为弘扬中华传统文化。某校开展双刚进课常”的活动。该校随机抽取部分学生,按四个类别:![]() 表示“很喜欢"
表示“很喜欢" ![]() 表示“喜欢”,
表示“喜欢”,![]() 表示"一般”,
表示"一般”,![]() 表示"不喜欢”.调查他们对汉剧的喜爱情况将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
表示"不喜欢”.调查他们对汉剧的喜爱情况将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
![]() 扇形统计图中.
扇形统计图中.![]() 类所对应的扇形圆心角的大小为 度;
类所对应的扇形圆心角的大小为 度;
![]() 请通过计算补全条形统计图:
请通过计算补全条形统计图:
![]() 该校共有
该校共有![]() 名学生.估计该校表示“很喜欢”的
名学生.估计该校表示“很喜欢”的![]() 类的学生有多少人?
类的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,若有两条中线互相垂直,则称该三角形为中垂三角形.
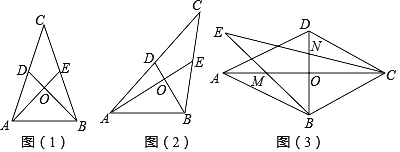
(1)如图(1),△ABC是中垂三角形,BD,AE分别是AC,BC边上的中线,且BD⊥AE于点O,若∠BAE=45°,求证:△ABC是等腰三角形.
(2)如图(2),在中垂三角形ABC中,AE,BD分别是边BC,AC上的中线,且AE⊥BD于点O,猜想AB2,BC2,AC2之间的数量关系,并加以证明.
(3)如图(3),四边形ABCD是菱形,对角线AC,BD交于点O,点M,N分别是OA,OD的中点,连接BM,CN并延长,交于点E.
①求证:△BCE是中垂三角形;
②若![]() ,请直接写出BE2+CE2的值.
,请直接写出BE2+CE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D在边BC上,点E在线段AD上.
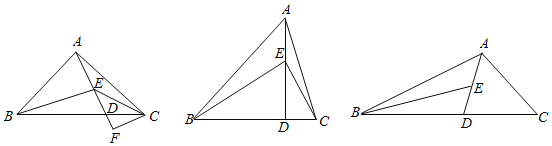
(1)若∠BAC=∠BED=2∠CED=α,
①若α=90°,AB=AC,过C作CF⊥AD于点F,求![]() 的值;
的值;
②若BD=3CD,求![]() 的值;
的值;
(2)AD为△ABC的角平分线,AE=ED=2,AC=5,tan∠BED=2,直接写出BE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com