
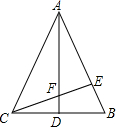
 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,在AB上取一点E,连接CE,交AD于点F.若BE=2,BC=6,∠CAD=∠BCE.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,在AB上取一点E,连接CE,交AD于点F.若BE=2,BC=6,∠CAD=∠BCE.分析 (1)根据等腰三角形的性质得到∠ACB=∠B,∠CAD=∠BAD,BD=CD=3,根据已知条件得到∠BEC=90°,推出△ABD∽△BCE,得到$\frac{AB}{BC}=\frac{BD}{BE}$,求得AB=9,结论即可得出;
(2)根据勾股定理得到CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=4$\sqrt{2}$,通过△DCF∽△BCE,求出DF=$\frac{3\sqrt{3}}{4}$,于是得到结果.
解答 解:(1)∵AB=AC,AD⊥BC,
∴∠ACB=∠B,∠CAD=∠BAD,BD=CD=3,
∵∠CAD=∠BCE,
∴∠BAD=∠BCE,
∴∠BAD+∠B=∠BCE+∠B=90°,
∴∠BEC=90°,
∴△ABD∽△BCE,
∴$\frac{AB}{BC}=\frac{BD}{BE}$,
∴$\frac{AB}{6}=\frac{3}{2}$,
∴AB=9.
∴AE=7;
(2)在Rt△BCE中,CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=4$\sqrt{2}$,
∵∠CDF=∠CEB=90°,∠DCF=∠BCE,∴△DCF∽△BCE,
∴$\frac{DF}{BE}=\frac{CD}{CE}$,
∴$\frac{DF}{2}=\frac{3}{4\sqrt{2}}$,
∴DF=$\frac{3\sqrt{3}}{4}$,
∴S△CDF=$\frac{1}{2}$CD•DF=$\frac{1}{2}×3×\frac{3\sqrt{2}}{4}$=$\frac{9\sqrt{2}}{8}$.
点评 本题考查了相似三角形的判定和性质,三角形的面积,勾股定理,熟练掌握相似三角形的判定和性质定理是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 1.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 1+$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
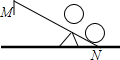 周末小威帮奶奶收拾菜园中的石头,有一块石头较大,需要借助木棒撬走,如图所示,O是支点,当用力压木棒的M端时,木棒绕点O转动,另一端N向上翘起,石头就被撬动.小威要想是这块石头滚动,木棒的N端必须向上跳起5cm.若3ON=OM,则要使这块石头滚动,至少要将木棒的M端向下压( )
周末小威帮奶奶收拾菜园中的石头,有一块石头较大,需要借助木棒撬走,如图所示,O是支点,当用力压木棒的M端时,木棒绕点O转动,另一端N向上翘起,石头就被撬动.小威要想是这块石头滚动,木棒的N端必须向上跳起5cm.若3ON=OM,则要使这块石头滚动,至少要将木棒的M端向下压( )| A. | 10cm | B. | 12cm | C. | 15cm | D. | 20cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3+4}$=$\sqrt{3}$+$\sqrt{4}$ | B. | $\sqrt{4-3}$=$\sqrt{4}$-$\sqrt{3}$ | C. | $\sqrt{{4}^{2}-{3}^{2}}$=4-3 | D. | $\sqrt{(4+3)^{2}}$=4+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com