
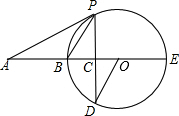
 如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.
如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.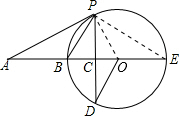 解:(1)证明:连接OP.
解:(1)证明:连接OP.| 2 |
| PC |
| CE |
| ||
| 2 |
| ||
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在我市初中学业水平考试体育科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线O-B-C-D,下列说法正确的是( )
如图,在我市初中学业水平考试体育科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线O-B-C-D,下列说法正确的是( )| A、小莹的速度随时间的增大而增大 |
| B、小梅的平均速度比小莹的平均速度大 |
| C、在起跑后86.4秒时,两人相遇 |
| D、在起跑后50秒内,小梅比小莹慢 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、5.49×1010元 |
| B、0.549×1011元 |
| C、54.9×1010元 |
| D、5.49×1011元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| x1 |
| x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com