
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①b2﹣4ac<0;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c=0;
④当y>0时,x的取值范围是﹣1<x<3;⑤当x>0时,y随x增大而减小.
其中结论正确的个数是( )
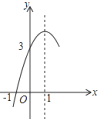
A.4个B.3个C.2个D.1个
【答案】B
【解析】
利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3,0),则可对②进行判断;由对称轴方程得到b=﹣2a,结合图象当x=-1时,y=0,则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断;根据二次函数的性质对⑤进行判断.
函数图象与x轴有2个交点,则b2﹣4ac>0,故①错误;
函数的对称轴是x=1,则与x轴的另一个交点是(3,0),
则方程ax2+bx+c=0的两个根是x1=﹣1,x2=3,故②正确;
函数的对称轴是x![]() 1,∴b=-2a,由图象可知:当x=-1时,y=a-b+c=0,∴a+2a+c=3a+c=0,故③正确;
1,∴b=-2a,由图象可知:当x=-1时,y=a-b+c=0,∴a+2a+c=3a+c=0,故③正确;
函数与x轴的交点是(﹣1,0)和(3,0)则当y>0时,x的取值范围是﹣1<x<3,故④正确;
当x>1时,y随x的增大而减小,则⑤错误.
故选B.


科目:初中数学 来源: 题型:
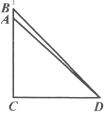
【题目】如图直线y=kx+k交x轴负半轴于点A,交y轴正半轴于点B,且AB=2
(1)求k的值;
(2)点P从A出发,以每秒1个单位的速度沿射线AB运动,过点P作直线AB的垂线交x轴于点Q,连接OP,设△PQO的面积为S,点P运动时间为t,求S与t的函数关系式,并直接写出t的取值范围;
(3)在(2)的条件下,当P在AB的延长线上,若OQ+AB=![]() (BQ﹣OP),求此时直线PQ的解析式.
(BQ﹣OP),求此时直线PQ的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中装有四个完全相同的小球,它们分别写有“美”“丽”、“椒”、“江”的文字.
(1)先从袋摸出1个球后放回,混合均匀后再摸出1个球,求两次摸出的球上是写有“美丽”二字的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球。求两次摸出的球上写有“椒江”二字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳阳超市以每件10元的价格购进了一批玩具,定价为20元时,平均每天可售出80个.经调查发现,玩具的单价每降1元,每天可多售出40个;玩具的单价每涨1元,每天要少售出5个.如何定价才能使每天的利润最大?求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京时间2019年3月10日0时28分,我国在西昌卫星发射中心用长征三号乙运载火箭,成功将中星![]() 卫星发射升空,卫星进入预定轨道.如图,火星从地面
卫星发射升空,卫星进入预定轨道.如图,火星从地面![]() 处发射,当火箭达到
处发射,当火箭达到![]() 点时,从位于地面雷达站
点时,从位于地面雷达站![]() 处测得
处测得![]() 的距离是
的距离是![]() ,仰角为
,仰角为![]() ;1秒后火箭到达
;1秒后火箭到达![]() 点,测得
点,测得![]() 的仰角为
的仰角为![]() .(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02)
.(参考数据:sin42.4°≈0.67,cos42.4°≈0.74,tan42.4°≈0.905,sin45.5°≈0.71,cos45.5°≈0.70,tan45.5°≈1.02)
(Ⅰ)求发射台与雷达站之间的距离![]() ;
;
(Ⅱ)求这枚火箭从![]() 到
到![]() 的平均速度是多少(结果精确到0.01)?
的平均速度是多少(结果精确到0.01)?
查看答案和解析>>
科目:初中数学 来源: 题型:
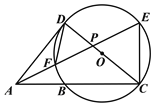
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
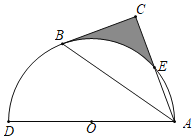
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E;B、E是半圆弧的三等分点,![]() 的长为
的长为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com