

分析 (1)由路程=速度×时间,结合题意列出方程,解方程即可得出结论;
(2)由路程=速度×时间,结合题意列出方程,解方程即可得出结论;
(3)若P、Q两点相遇,则相遇时点P在直线上,由P点的旋转速度可找出当P在直线上时的时间,再由路程=速度×时间,列出一元一次方程,解方程即可得出结论.
解答 解:(1)设经过x分钟后,P、Q两点相遇,依题意得:
4x+6x=60,解得:x=6.
答:经过6分钟后,P、Q两点相遇.
(2)设经过y分钟后,P、Q两点相距20厘米,依题意得:
①4y+6y+20=60,解得:y=4;
②4y+6y-20=60,解得:y=8.
答:经过4或8分钟后,P、Q两点相距20厘米.
(3)由题意知,点P、Q只能在直线AB上相遇,则点P旋转到直线上的时间为2分钟或11分钟.
设点Q的速度为t厘米/分,依题意得:
①2t=60-16,解得:t=22;
②11t=60,解得:t=$\frac{60}{11}$.
答:点Q的速度为22厘米/分或$\frac{60}{11}$厘米/分.
点评 本题考查了一元一次方程的应用,解题的关键是结合路程=速度×时间与题意,列出一元一次方程.本题属于基础题,难度不大,解决该类问题时,理清各数量之间的关系式关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
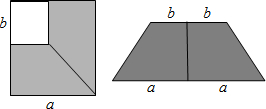
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x+1 | B. | $y=\frac{1}{3x}$ | C. | $y=\frac{1}{x-5}$ | D. | y=$\frac{2}{{x}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com