
分析 根据长方形的面积等于长乘以宽,由长方形的面积为xy-1-x+y,其中一边长为y-1,可以求得另一边的长,然后根据长方形的周长等于长加宽的和乘以2,从而本题得以解决.
解答 解:∵一个长方形的面积为xy-1-x+y,其中一边长为y-1,
∴长方形的另一边长为:(xy-1-x+y)÷(y-1)=$\frac{(xy-x)+(y-1)}{y-1}$=$\frac{x(y-1)+(y-1)}{y-1}=\frac{(x+1)(y-1)}{y-1}$=x+1,
∴该长方形的周长是:[(y-1)+(x+1)]×2=(y-1+x+1)×2=2y+2x,
即该长方形的周长是2x+2y.
点评 本题考查整式的除法、长方形的面积和周长,解题的关键是明确题意,知道长方形的周长和面积公式.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
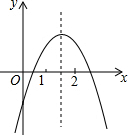 一次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;
一次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
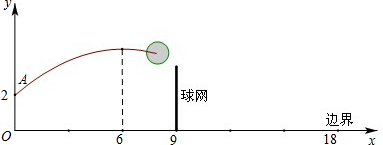
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com