
分析 设x-y=a,y-z=b,x-z=c,得出a+b=x-z=-c,代入后通分,再变形,即可得出答案.
解答 解:设x-y=a,y-z=b,x-z=c,
则a+b=x-z=-c,
$\frac{(y-z)^{2}}{(x-y)(x-z)}$+$\frac{(z-x)^{2}}{(y-x)(y-z)}$+$\frac{(x-y)^{2}}{(z-x)(z-y)}$
=$\frac{{b}^{2}}{ac}$+$\frac{(-c)^{2}}{-ab}$+$\frac{{a}^{2}}{(-c)•(-b)}$
=$\frac{{b}^{2}}{ac}$-$\frac{{c}^{2}}{ab}$+$\frac{{a}^{2}}{bc}$
=$\frac{{b}^{3}-{c}^{3}+{a}^{3}}{abc}$
=$\frac{(a+b)({a}^{2}-ab+{b}^{2})-{c}^{3}}{abc}$
=$\frac{-c({a}^{2}-ab+{b}^{2})-{c}^{3}}{abc}$
=-$\frac{{a}^{2}-ab+{b}^{2}+{c}^{2}}{ab}$
=-$\frac{{a}^{2}-ab+{b}^{2}+[-(a+b)^{2}]}{ab}$
=-$\frac{2{a}^{2}+ab+2{b}^{2}}{ab}$
=-$\frac{2(x-y)^{2}+(x-y)(y-z)+2(y-z)^{2}}{(x-y)(y-z)}$
=$\frac{2{x}^{2}-3xy+3{y}^{2}-xz-3yz+2{z}^{2}}{xy-xz-{y}^{2}+yz}$.
点评 本题考查了分式的加减的应用,能选择适当的方法进行计算是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,1) | B. | (-1,1) | C. | (-1,-1) | D. | (-3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
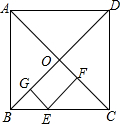 如图,在正方形ABCD中,对角线AC、BD交于O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G、F,AC=10,则EG+EF=5.
如图,在正方形ABCD中,对角线AC、BD交于O,E点在BC上,EG⊥OB,EF⊥OC,垂足分别为点G、F,AC=10,则EG+EF=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com