
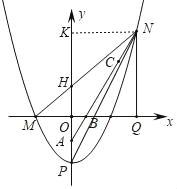
【题目】如图1,抛物线C1:y=ax2+k的顶点A(0,﹣2),且过点(2,0),点B的坐标为(1,0),直线AB交抛物线C1于另一点C.

(1)抛物线的解析式为 ;
(2)求点C的坐标:
(3)如图2,将抛物线C1向下平移m(m>0)个单位得到抛物线C,且抛物线C的顶点为P,交x轴负半轴于点M,交射线BC于点N,NQ⊥x轴于点Q,当NP平分∠MNQ时,求m的值.
【答案】(1)y=![]() x2﹣2;(2)C(4,6);(3)2.
x2﹣2;(2)C(4,6);(3)2.
【解析】
(1)根据抛物线过点A求出k法人值,再根据线上的另一点(2,0)求出a,将求得的a与k代入,求得解析式
(2)先利用A、B两点坐标,以待定系数法求出直线AB的解析式,再利用方程组求得两个函数图像的交点坐标,根据实际情况判断出交点坐标的正确取值范围即可
(3)分别设出抛物线C2表达式为:y=![]() x2﹣2﹣m,点M坐标为(n,0),则C2表达式
x2﹣2﹣m,点M坐标为(n,0),则C2表达式
为:y=![]() x2﹣
x2﹣![]() n2,结合(2)中求出的直线AB的表达式得出点N(2﹣n,2﹣2n),从而知道△MNQ为等腰直角三角形;再设直线MN与y轴的交点为H,并作NK⊥y轴于点K,进一步得出NH=HP,再建立方程求出n从而得出m的值
n2,结合(2)中求出的直线AB的表达式得出点N(2﹣n,2﹣2n),从而知道△MNQ为等腰直角三角形;再设直线MN与y轴的交点为H,并作NK⊥y轴于点K,进一步得出NH=HP,再建立方程求出n从而得出m的值
解:(1)抛物线C1:的顶点A(0,﹣2),则k=﹣2,
则y=ax2﹣2,将点(2,0)代入上式得:0=a(2)2﹣2,
解得:a=![]() ,
,
则抛物线的表达式:y=![]() x2﹣2…①,
x2﹣2…①,
故答案为:y=![]() x2﹣2;
x2﹣2;
(2)将点A、B的坐标代入y=kx+b得![]() ,解得:
,解得:![]() ,
,
故直线AB的表达式为:y=2x﹣2…②,
联立①②并解得:x=0或4(舍去0),
故点C(4,6);
(3)设抛物线C2表达式为:y=![]() x2﹣2﹣m,设点M(n,0),
x2﹣2﹣m,设点M(n,0),
则![]() n2﹣2﹣m=0,抛物线C2表达式为:y=
n2﹣2﹣m=0,抛物线C2表达式为:y=![]() x2﹣
x2﹣![]() n2…③,
n2…③,
联立②③并解得:x=2﹣n或2+n,则点N(2﹣n,2﹣2n),
则NQ=2﹣2n,MQ=2﹣2n,
∴△MNQ为等腰直角三角形,则∠MNQ=45°,
又点P(0,﹣![]() n2),即点M(n,0),
n2),即点M(n,0),
设直线MN与y轴的交点为H,则OH=OM,则点H(0,﹣n),
作NK⊥y轴于点K,在△NKH中,NK=KH,
则NH=![]() (2﹣n),又HP=OH+OP=
(2﹣n),又HP=OH+OP=![]() n2﹣n,
n2﹣n,
∵PN为角平分线,则∠MNP=∠PNQ=22.5°,
故NH=HP,
则![]() (2﹣n)=
(2﹣n)=![]() n2﹣n,
n2﹣n,
解得:n=2或﹣2![]() (舍去2),
(舍去2),
∵![]() n2﹣2﹣m=0,解得:m=2.
n2﹣2﹣m=0,解得:m=2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
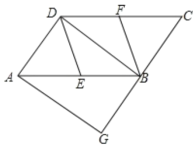
【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜂蜜具有消食、润肺、安神、美颜之功效,是天然的健康保健佳品.秋天即将来临时,雪宝山土特产公司抓住商机购进甲、乙、丙三种蜂蜜,已知销售每瓶甲蜂蜜的利润率为10%,每瓶乙蜂蜜的利润率为20%,每瓶丙蜂蜜的利润率为30%.当售出的甲、乙、丙蜂蜜瓶数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙蜂蜜瓶数之比为3:2:1时,商人得到的总利润率为20%.那么当售出的甲、乙、丙蜂蜜瓶数之比为5:6:1时,该公司得到的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.

(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
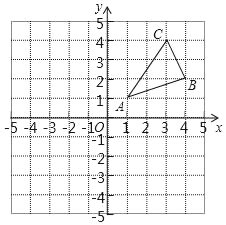
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
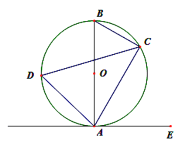
(1)求证:AE是⊙O的切线;
(2) 连接OC,当BC=3时,求劣弧AC的长和扇形B0C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
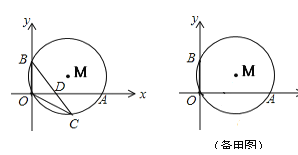
【题目】如图,⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程![]() 的两根.
的两根.
(1)求线段OA、OB的长;
(2)若点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求点C的坐标;
(3)若点C在优弧OA上,作直线BC交x轴于D,是否存在△COB和△CDO相似,若存在,求出点C的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在促销活动中规定,顾客每消费100元就能获得一次抽奖机会.为了活跃气氛,设计了两个抽奖方案:
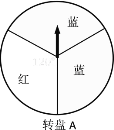
方案一:转动转盘A一次,转出红色可领取一份奖品;
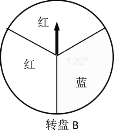
方案二:转动转盘B两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)如果你获得一次抽奖机会,你会选择哪个方案?请用相关的数学知识说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com