
【题目】如图,⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程![]() 的两根.
的两根.
(1)求线段OA、OB的长;
(2)若点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求点C的坐标;
(3)若点C在优弧OA上,作直线BC交x轴于D,是否存在△COB和△CDO相似,若存在,求出点C的坐标,若不存在,请说明理由.
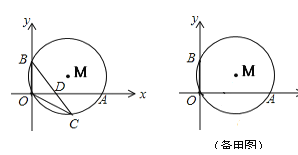
【答案】(1)OA=12,OB=5;(2)C点坐标为(6,-4);(3)存在. C点坐标为(6,9).
【解析】
(1)利用因式分解法解方程即可得到OA=12,OB=5;
(2)连接AB、AC、MC,MC与OA交于F,如图1,由OC2=CDCB,∠OCD=∠BCO,根据相似三角形的判定方法即可得到△COD∽△CBO,则∠2=∠1,而根据圆周角定理有∠1=∠3,所以∠2=∠3,得到弧AC=弧OC,根据垂径定理得MC⊥OA,OF=AF=![]() OA=6,然后根据圆周角定理由∠AOB=90°得AB为⊙M的直径,则在Rt△AOB中,根据勾股定理可计算出AB=13,得到MC=
OA=6,然后根据圆周角定理由∠AOB=90°得AB为⊙M的直径,则在Rt△AOB中,根据勾股定理可计算出AB=13,得到MC=![]() ,易得MF=
,易得MF=![]() OB=
OB=![]() ,则FC=MC-MF=4,于是得到C点坐标为(6,-4);
,则FC=MC-MF=4,于是得到C点坐标为(6,-4);
(3)连接AC,连接CM并延长交OA于F,如图2,若CA=CO,则∠COA=∠CAO,根据邻补角的定义得∠COA+∠COD=180°,根据圆内接四边形的性质得∠CAO+∠CBO=180°,则∠COD=∠CBO,加上∠OCD=∠DCO,根据相似的判定方法即可得到△CBO∽△COD;由CA=CO得弧CA=弧CO,根据垂径定理得CF⊥AC,由(2)得MF=![]() ,CM=
,CM=![]() ,OF=6,则CF=CM+MF=9,于是得到C点坐标为(6,9).
,OF=6,则CF=CM+MF=9,于是得到C点坐标为(6,9).
(1)∵(x-12)(x-5)=0,
∴x1=12,x2=5,
∴OA=12,OB=5;
(2)连接AB、AC、MC,MC与OA交于F,如图1,

∵OC2=CDCB,即OC:CD=CB:OC,
而∠OCD=∠BCO,
∴△COD∽△CBO,
∴∠2=∠1,
∵∠1=∠3,
∴∠2=∠3,
∴弧AC=弧OC,
∴MC⊥OA,
∴OF=AF=![]() OA=6,
OA=6,
∵∠AOB=90°,
∴AB为⊙M的直径,
在Rt△AOB中,OA=12,OB=5,
∴AB=13,
∴MC=![]() ,
,
∵MF为△AOB的中位线,
∴MF=![]() OB=
OB=![]() ,
,
∴FC=MC-MF=4,
∴C点坐标为(6,-4);
(3)存在.
连接AC,连接CM并延长交OA于F,如图2,
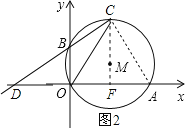
若CA=CO,则∠COA=∠CAO,
∵∠COA+∠COD=180°,∠CAO+∠CBO=180°,
∴∠COD=∠CBD,而∠OCD=∠DOC,
∴△CBO∽△COD,
∵CA=CO,
∴弧CA=弧CO,
∴CF⊥AC,
由(2)得MF=![]() ,CM=
,CM=![]() ,OF=6,
,OF=6,
∴CF=CM+MF=9,
∴C点坐标为(6,9).


科目:初中数学 来源: 题型:
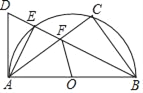
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且∠DAE=∠FAE.
(1)求证:AD为⊙O切线;
(2)若sin∠BAC=![]() ,求tan∠AFO的值.
,求tan∠AFO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C1:y=ax2+k的顶点A(0,﹣2),且过点(2,0),点B的坐标为(1,0),直线AB交抛物线C1于另一点C.

(1)抛物线的解析式为 ;
(2)求点C的坐标:
(3)如图2,将抛物线C1向下平移m(m>0)个单位得到抛物线C,且抛物线C的顶点为P,交x轴负半轴于点M,交射线BC于点N,NQ⊥x轴于点Q,当NP平分∠MNQ时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (
(![]() >0)与一次函数
>0)与一次函数![]() 的图像交于B,C两点,一次函数
的图像交于B,C两点,一次函数![]() 图像与y轴交于点A.
图像与y轴交于点A.


(1)当k=3,a+b=4时,
①求B,C两点的坐标;
②求△OBC的面积![]() ;
;
(2)当k=1时,设B、C两点坐标为 B(a,b)(a≥2)、C(c,d)(点B、C不重合).
①求ac的值;
②设△OAC面积为![]() ,求
,求![]() 与b的函数关系式,并直接写出
与b的函数关系式,并直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的不断提高,越来越多的人选择到电影院观看电影,体验视觉盛宴,并且更多的人通过网上平台购票,既快捷又能享受更多优惠.某电影城2019年从网上购买![]() 张电影票的费用比现场购买
张电影票的费用比现场购买![]() 张电影票的费用少
张电影票的费用少![]() 元:从网上购买
元:从网上购买![]() 张电影票的费用和现场购买
张电影票的费用和现场购买![]() 张电影票的费用共
张电影票的费用共![]() 元.
元.
(1)求该电影城2019年在网上购票和现场购票每张电影票的价格为多少元?
(2)2019年五一当天,该电影城按照2019年网上购票和现场购票的价格销售电影票,当天售出的总票数为![]() 张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低
张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低![]() 元,售出总票数就比五一当天增加
元,售出总票数就比五一当天增加![]() 张.经统计,5月5日售出的总票数中有
张.经统计,5月5日售出的总票数中有![]() 的电影票通过网上售出,其余通过现场售出,且当天票房总收入为
的电影票通过网上售出,其余通过现场售出,且当天票房总收入为![]() 元,试求出5月5日当天现场购票每张电影票的价格为多少元?
元,试求出5月5日当天现场购票每张电影票的价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于![]() ,超过
,超过![]() 时,所有这种水果的批发单价均为3元
时,所有这种水果的批发单价均为3元![]() .图中折线表示批发单价
.图中折线表示批发单价![]() (元
(元![]() )与质量
)与质量![]() 的函数关系.
的函数关系.
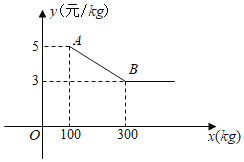
(1)求图中线段![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)小李用800元一次可以批发这种水果的质量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com