
【题目】如图,菱形![]() 中,一射线
中,一射线![]() 分
分![]() 为
为![]() 与
与![]() ,且
,且![]() ,
,![]() 交对角线
交对角线![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() 点,交
点,交![]() 于
于![]() ,且
,且![]() ,
,
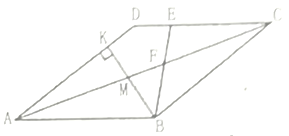
(1)求![]() 的度数;
的度数;
(2)求证:![]() .
.
【答案】(1)75;(2)见解析
【解析】
(1)根据菱形的对角线平分一组对角线可得∠BAD=2∠DAC,然后求出∠ABC,再根据比例求出∠ABE,然后根据两直线平行,同旁内角互补求解即可;
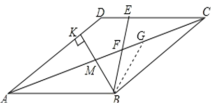
(2)根据两直线平行,内错角相等可得∠CBM=∠AKB=90°,取CM的中点G,连接BG,根据直角三角形斜边上的中线等于斜边的一半可得BG=CG=![]() CM,再根据等边对等角求出∠CBG=∠BCG=15°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BGM=30°,再求出∠GBF=30°,从而得到∠GBF=∠BMG,根据等角对等边可得FB=FG,然后根据CF=CG+FG代入整理即可得证.
CM,再根据等边对等角求出∠CBG=∠BCG=15°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BGM=30°,再求出∠GBF=30°,从而得到∠GBF=∠BMG,根据等角对等边可得FB=FG,然后根据CF=CG+FG代入整理即可得证.
(1)![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)证明:![]() ,菱形的对边
,菱形的对边![]() ,
,
![]() ,
,![]() ,
,
如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
则![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
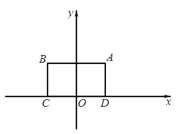
【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(![]() ,
,![]() ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.
(1)当⊙P的半径为4时,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
②如果点P在直线![]() 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
(2)已知点P在![]() 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月饼是久负盛名的中国传统糕点之一,宋代大诗人苏东坡有诗句“小饼如嚼月,中有酥和饴”赞美月饼.为满足市场需求,某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不低于45元且不超过58元,根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量![]() (盒)与每盒售价
(盒)与每盒售价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
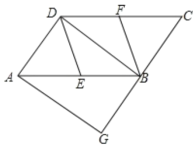
【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
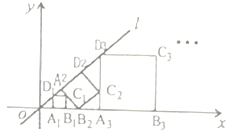
【题目】如图,在平面直角坐标系中,直线![]() 为正比例函数
为正比例函数![]() 的图象,点
的图象,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 轴于点
轴于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,…,按此规律操作下所得到的正方形
,…,按此规律操作下所得到的正方形![]() 的面积是
的面积是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,将![]() 沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
(1)若点D恰好与点O重合,则∠ABC= °;
(2)延长CD交⊙O于点M,连接BM.猜想∠ABC与∠ABM的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜂蜜具有消食、润肺、安神、美颜之功效,是天然的健康保健佳品.秋天即将来临时,雪宝山土特产公司抓住商机购进甲、乙、丙三种蜂蜜,已知销售每瓶甲蜂蜜的利润率为10%,每瓶乙蜂蜜的利润率为20%,每瓶丙蜂蜜的利润率为30%.当售出的甲、乙、丙蜂蜜瓶数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙蜂蜜瓶数之比为3:2:1时,商人得到的总利润率为20%.那么当售出的甲、乙、丙蜂蜜瓶数之比为5:6:1时,该公司得到的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
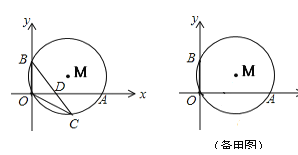
【题目】如图,⊙M经过O点,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长是方程![]() 的两根.
的两根.
(1)求线段OA、OB的长;
(2)若点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求点C的坐标;
(3)若点C在优弧OA上,作直线BC交x轴于D,是否存在△COB和△CDO相似,若存在,求出点C的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com