


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
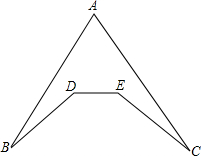 某天,王梦洁从B村出发到C村找董倩,由于B村到C村之间有一小山,不能直接到达,现有两条路线可以选择,如图,一条路线是BDEC,另一条路线是BAC,请你就上述两条路线选择用一条从B村到C村的较近路线.
某天,王梦洁从B村出发到C村找董倩,由于B村到C村之间有一小山,不能直接到达,现有两条路线可以选择,如图,一条路线是BDEC,另一条路线是BAC,请你就上述两条路线选择用一条从B村到C村的较近路线.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm.
如图,AB是⊙O的直径,动弦CD垂直AB于点E,过点B作直线BF∥CD交AD的延长线于点F,若AB=10cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com