
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,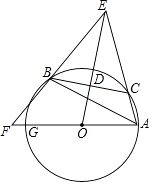
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
【答案】
(1)
解:β=α+90°,γ=﹣α+180°
连接OB,

∴由圆周角定理可知:2∠BCA=360°﹣∠BOA,
∵OB=OA,
∴∠OBA=∠OAB=α,
∴∠BOA=180°﹣2α,
∴2β=360°﹣(180°﹣2α),
∴β=α+90°,
∵D是BC的中点,DE⊥BC,
∴OE是线段BC的垂直平分线,
∴BE=CE,∠BED=∠CED,∠EDC=90°
∵∠BCA=∠EDC+∠CED,
∴β=90°+∠CED,
∴∠CED=α,
∴∠CED=∠OBA=α,
∴O、A、E、B四点共圆,
∴∠EBO+∠EAG=180°,
∴∠EBA+∠OBA+∠EAG=180°,
∴γ+α=180°
(2)
解:当γ=135°时,此时图形如图所示,
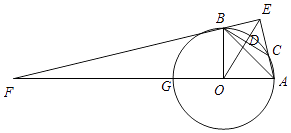
∴α=45°,β=135°,
∴∠BOA=90°,∠BCE=45°,
由(1)可知:O、A、E、B四点共圆,
∴∠BEC=90°,
∵△ABE的面积为△ABC的面积的4倍,
∴ ![]() ,
,
∴ ![]() ,
,
设CE=3x,AC=x,
由(1)可知:BC=2CD=6,
∵∠BCE=45°,
∴CE=BE=3x,
∴由勾股定理可知:(3x)2+(3x)2=62,
x= ![]() ,
,
∴BE=CE=3 ![]() ,AC=
,AC= ![]() ,
,
∴AE=AC+CE=4 ![]() ,
,
在Rt△ABE中,
由勾股定理可知:AB2=(3 ![]() )2+(4
)2+(4 ![]() )2,
)2,
∴AB=5 ![]() ,
,
∵∠BAO=45°,
∴∠AOB=90°,
在Rt△AOB中,设半径为r,
由勾股定理可知:AB2=2r2,
∴r=5,
∴⊙O半径的长为5.
【解析】(1)由圆周角定理即可得出β=α+90°,然后根据D是BC的中点,DE⊥BC,可知∠EDC=90°,由三角形外角的性质即可得出∠CED=α,从而可知O、A、E、B四点共圆,由圆内接四边形的性质可知:∠EBO+∠EAG=180°,即γ=﹣α+180°;(2)由(1)及γ=135°可知∠BOA=90°,∠BCE=45°,∠BEC=90°,由于△ABE的面积为△ABC的面积的4倍,所以 ![]() ,根据勾股定理即可求出AE、AC的长度,从而可求出AB的长度,再由勾股定理即可求出⊙O的半径r;
,根据勾股定理即可求出AE、AC的长度,从而可求出AB的长度,再由勾股定理即可求出⊙O的半径r;
【考点精析】通过灵活运用余角和补角的特征和三角形的面积,掌握互余、互补是指两个角的数量关系,与两个角的位置无关;三角形的面积=1/2×底×高即可以解答此题.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
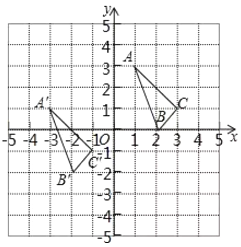
(1)分别写出各点的坐标:![]() ___________,
___________,![]() _________,
_________,![]() _______________.
_______________.
(2)![]() 是由
是由![]() 经过怎样的平移变换得到的?答:___________________.
经过怎样的平移变换得到的?答:___________________.
(3)若点![]() 是
是![]() 内部一点,则
内部一点,则![]() 内部的对应点
内部的对应点![]() 的坐标为___________.
的坐标为___________.
(4)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
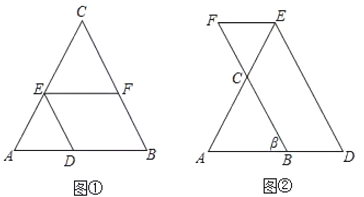
(1)如图①,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的度数.请将下面的解答过程补充完整,并填空.
的度数.请将下面的解答过程补充完整,并填空.
(1)解:
![]() ,
,
![]() (两直线平行,内错角相等).
(两直线平行,内错角相等).
![]() ,
,
![]() (___________________________________).
(___________________________________).
![]() (__________________).
(__________________).
![]() .
.
应用:
(2)如图②,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 的延长线上,且
的延长线上,且![]() ,
,![]() ,若
,若,求
![]() 的大小.(用含
的大小.(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为y(米)与时间x(分钟)的关系如图.请结合图象,解答下列问题:
(1)填空:a=________;b=________;m=________.
(2)若小军的速度是 120 米/分,求小军第二次与爸爸相遇时距图书馆的距离.
(3)在(2)的条件下,爸爸自第二次出发后,骑行一段时间后与小军相距100 米,此时 小军骑行的时间为________分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com