Question

5．如图，在Rt△ABC中，∠C=90°，AC=BC=6，点D为AC中点，点E为边AB上一动点，点F为射线BC上一动点，且∠FDE=90°．
（1）当DF∥AB时，联结EF，求DE：DF值；
（2）当点F在线段BC上时，设AE=x，BF=y，求y关于x的函数关系式，并写出x的取值范围；
（3）联结CE，若△CDE为等腰三角形，求BF的长．

Answer 1

分析 （1）先根据勾股定理求出AB的长，再由三角形的中位线定理求出DF、DE的长，即可求出DE：DF值；
（2）过点E作EH⊥AC于点H，由平行线的性质及等腰三角形的性质可求出HE、HD的表达式，再由相似三角形的判定定理求出△HDE∽△CFD，根据相似三角形的性质可写出y关于x的函数关系式；
（3）先分析出△DCE为等腰三角形时的两种情况，再根据题意画出图形，当DC=DE时，点F在边BC上，过点D作DG⊥AE于点G，可求出AE的长度，由AE的长可判断出F的位置，进而可求出BF的长；当ED=EC时，先判断出点F的位置，再根据相似三角形的性质及判定定理即可解答．

解答 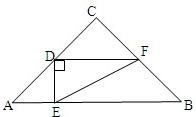解：（1）∴AC=BC=6，∠ACB=90°，
∴$AB=6\sqrt{2}$，
∵DF∥AB，$CD=\frac{1}{2}AC$，
∴$DF=\frac{1}{2}AB=3\sqrt{2}$，
∴$DE=\frac{3}{2}\sqrt{2}$，
∴在Rt△DEF中，$\frac{DE}{DF}$=$\frac{\frac{3}{2}\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{2}$；

（2）过点E作EH⊥AC于点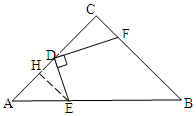，则$HE=HA=\frac{{\sqrt{2}}}{2}x$，
∴$HD=3-\frac{{\sqrt{2}}}{2}x$，
根据∠DHE=∠C=90°，∠DEH=∠FDC，可得△HDE∽△CFD，
∴$\frac{HD}{CF}=\frac{HE}{DC}$，
∴$\frac{{3-\frac{{\sqrt{2}}}{2}x}}{6-y}=\frac{{\frac{{\sqrt{2}}}{2}x}}{3}$，
∴$y=-\frac{{9\sqrt{2}}}{x}+9$$（\sqrt{2}＜x≤3\sqrt{2}）$；

（3）∵$CE≥\frac{1}{2}AB=3\sqrt{2}＞3$，CD=3，
∴CE＞CD，
∴若△DCE为等腰三角形，只有DC=DE或ED=EC两种可能：
①当DC=DE时，点F在边BC上，
过点D作DG⊥AE于点G（如图①），
可得：$AE=2AG=3\sqrt{2}$，
即点E在AB中点，
∴此时F与C重合，
∴BF=6；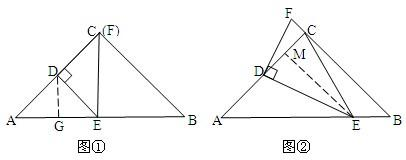
②当ED=EC时，点F在BC的延长线上，
过点E作EM⊥CD于点M（如图②），
可证：△DFC∽△DEM，
∴$\frac{CF}{DM}=\frac{CD}{EM}$，
∴$\frac{CF}{{\frac{3}{2}}}=\frac{3}{{3+\frac{3}{2}}}$，
∴CF=1，
∴BF=7，
综上所述，BF为6或7．

点评 本题主要考查了是一道综合题，涉及到锐角三角函数的定义、直角三角形的性质、相似三角形的判定与性质，涉及面较广，难度较大．运用分类讨论的思想是解决本题的关键．