
【题目】如图,已知点 A(-1,0)和点B(1,2) ,在 y 轴正半轴上确定点 P ,使得△ABP 为直角三角形,则满足条件的点 P 的坐标为 . 
【答案】(0,3)或(0,1+![]() ).
).
【解析】①如下图,
过点B作BP⊥AB,交y轴于点P,过点B作BD⊥OP,交OP于点D,
∴∠ABP=90°,BD=1,
∵点 A(-1,0),点B(1,2) 在直线AB上,
∴直线AB的函数解析式为:y=x+1,
∴点C(0,1),
即OC=1=OA,
∴![]() AOC是等腰三角形,
AOC是等腰三角形,
∴∠ACO=∠BCP=45°,
∴![]() BCP是等腰直角三角形,
BCP是等腰直角三角形,
∴CP=2BD=2,
∴OP=3,
即点P的坐标为(0,3).
②如下图:
当∠APB=90°时,
∵点 A(-1,0),点B(1,2),点C(0,1),
∴点C为AB的中点,AB=![]() ,
,
∴CP=![]() AB=
AB=![]() ,
,
∴OP=1+![]() ,
,
∴点P(0,1+![]() ),
),
综上,点P的坐标为(0,3)或(0,1+![]() ).
).
所以答案是:(0,3)或(0,1+![]() ).
).
【考点精析】解答此题的关键在于理解勾股定理的逆定理的相关知识,掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】反比例函数y1= ![]() (a>0,a为常数)和y2=
(a>0,a为常数)和y2= ![]() 在第一象限内的图象如图所示,点M在y2=
在第一象限内的图象如图所示,点M在y2= ![]() 的图象上,MC⊥x轴于点C,交y1=
的图象上,MC⊥x轴于点C,交y1= ![]() 的图象于点A;MD⊥y轴于点D,交y1=
的图象于点A;MD⊥y轴于点D,交y1= ![]() 的图象于点B,当点M在y2=
的图象于点B,当点M在y2= ![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积为2﹣a;
③当a=1时,点A是MC的中点;
④若S四边形OAMB=S△ODB+S△OCA , 则四边形OCMD为正方形.
其中正确的是 . (把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A,C分别在x轴,y轴的正半轴上,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.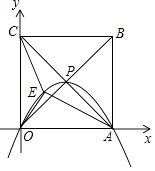
(1)点P的坐标为;
(2)求抛物线L的解析式;
(3)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶替换原来的垃圾桶,![]() ,
,![]() ,
,![]() 三个小区所购买的数量和总价如表所示.
三个小区所购买的数量和总价如表所示.
甲型垃圾桶数量(套) | 乙型垃圾桶数量(套) | 总价(元) | |
|
|
|
|
|
|
|
|
|
|
|
|
(1)问甲型垃圾桶、乙型垃圾桶的单价分别是每套多少元?
(2)求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感恩是中华民族的传统美德,在4月份某校提出了“感恩父母、感恩老师、感恩他人”的“三感”教育活动.感恩事例有:A.给父母过一次生日;B .为父母做一次家务活,让父母休息一天;C.给老师一个发自内心的拥抱,并且与老师谈心;D.帮助有困难的同学度过难关.为了解学生对这四种感恩事例的情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学在4种感恩事例中选择最想做的一种),将数据进行整理并绘制成以下两幅统计图(未画完整).
(1)这次调查中,一共查了名学生;
(2)请补全扇形统计图中的数据及条形统计图;
(3)若有3名选 A的学生,1名选 C的学生组成志愿服务队外出参加联谊活动,欲从中随机选出2人担任活动负责人,请通过树状图或列表求两人均是选 A的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福田区某轿车销售公司为龙泉工业区代销 A 款轿车,为了吸引购车族,销售公司打出降价牌,今年 5月份A款轿车每辆售价比去年同期每辆售价低 1万元,如果卖出相同数量的 A 款轿车,去年的销售额为100万元,今年销售额只有90万元.
(1)今年 5月份 A 款轿车每辆售价为多少元?
(2)为了增加收入,该轿车公司决定再为龙泉工业区代销 B款轿车,已知 A款轿车每辆进价为 7.5万元,B款轿车每辆进价为 6万元,公司预计用不多于105万元的资金购进这两款轿车共 15 辆,但A款轿车不多于6辆,试问共有几种进货方案?
(3)在⑵的条件下,B款轿车每辆售价为 8万元,为打开B款轿车的销路,公司决定每售出一辆 B款轿车,返还顾客现金a( 0<a ≤1 )万元.假设购进的15辆车能够全部卖出去,试讨论采用哪种进货方案可以使该轿车销售公司卖出这 15辆车后获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C(﹣3,0),点A,B分别在x轴,y轴的正半轴上,且满足 ![]() +|OA﹣1|=0
+|OA﹣1|=0
(1)求点A,点B的坐标.
(2)若点P从C点出发,以每秒1个单位的速度沿射线CB运动,连结AP.设△ABP的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点P,使以点A,B,P为顶点的三角形与△AOB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com