
| A. | 若2x=a,则x=2a | B. | 若$\frac{x}{2}$+$\frac{x}{3}$=1,则3x+2x=1 | ||
| C. | 若ab=bc,则a=c | D. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b |
分析 根据等式的性质进行判断.
解答 解:A、在等式2x=a的两边同时除以2,等式仍成立,即x=$\frac{1}{2}$a.故本选项错误;
B、在等式$\frac{x}{2}$+$\frac{x}{3}$=1的两边同时乘以6,等式仍成立,即3x+2x=6.故本选项错误;
C、当b=0时,a=c不一定成立,故本选项错误;
D、在等式$\frac{a}{c}$=$\frac{b}{c}$的两边同时乘以c,等式仍成立,即a=b,故本选项正确;
故选:D.
点评 本题考查了等式的性质.
性质1等式两边加同一个数(或式子)结果仍得等式;
性质2:等式两边乘同一个数或除以一个不为零的数,结果仍得等式.


科目:初中数学 来源: 题型:解答题
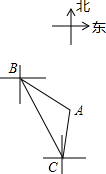 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,求C处与灯塔A的距离.
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,求C处与灯塔A的距离.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
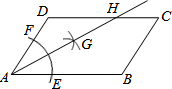 如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论正确的有:①③.
如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论正确的有:①③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)解不等式组:$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,并把解集在数轴上表示出来.
(1)解不等式组:$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,并把解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com