
【题目】如图,在△ABC中,点P,Q分别在BC,AC上,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下面结论错误是( )
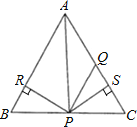
A. △BPR≌△QPSB. AS=ARC. QP∥ABD. ∠BAP=∠CAP
【答案】A
【解析】
根据到角的两边的距离相等的点在角的平分线上可得AP平分∠BAC,从而判断出A正确,然后根据等边对等角的性质可得∠APQ=∠PAQ,然后得到∠APQ=∠PAR,然后根据内错角相等两直线平行可得QP∥AB,从而判断出C正确,然后证明出△APR与△APS全等,根据全等三角形对应边相等即可得到B正确,C中两三角形只能确定一直角边相等,已知角相等,其他条件都无法确定,所以不一定正确.
解:∵PR⊥AB于点R,PS⊥AC于点S,且PR=PS,
∴点P在∠BAC的平分线上,
即AP平分∠BAC,故A正确;
∴∠PAR=∠PAQ,
∵AQ=PQ,
∴∠APQ=∠PAQ,
∴∠APQ=∠PAR,
∴QP∥AB,故C正确;
在Rt△APR与Rt△APS中,![]()
∴Rt△APR≌Rt△APS(HL),
∴AR=AS,故B正确;
△BPR和△QSP只能知道PR=PS,∠BRP=∠QSP=90°,其他条件不容易得到,所以,不一定全等.
故D错误.
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
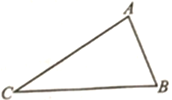
【题目】如图,△ABC中,AC=8,BC=10,AC>AB.
(1)用尺规作图法在△ABC内求作一点D,使点D到两点A、C的距离相等,又到边AC、BC的距离相等(保留作图痕迹,不写作法).
(2)若△ACD的周长为18,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合“一带一路”国家倡议,某铁路货运集装箱物流园区正式启动了2期扩建工程一项地基基础加固处理工程由2、8两个工程公司承担建设,己知2工程公司单独建设完成此项工程需要180天![]() 工程公司单独施工天后,
工程公司单独施工天后,![]() 工程公司参与合作,两工程公司又共同施工
工程公司参与合作,两工程公司又共同施工![]() 天后完成了此项工程.
天后完成了此项工程.
(1)求![]() 工程公司单独建设完成此项工程需要多少天?
工程公司单独建设完成此项工程需要多少天?
(2)由于受工程建设工期的限制,物流园区管委会决定将此项工程划包成两部分,要求两工程公司同时开工,![]() 工程公司建设其中一部分用了
工程公司建设其中一部分用了![]() 天完成,
天完成,![]() 工程公司建设另一部分用了
工程公司建设另一部分用了![]() 天完成,其中
天完成,其中![]() ,
,![]() 均为正整数,且
均为正整数,且![]() ,
,![]() ,求
,求![]() 、
、![]() 两个工程公司各施工建设了多少天?
两个工程公司各施工建设了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
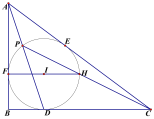
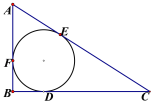
【题目】如图, Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F, (1)设AB=c, BC=a, AC=b, 求证: 内切圆半径r=![]() (a+b-c).
(a+b-c).
(2) 若AD交圆于P, PC交圆于H, FH//BC, 求∠CPD;
(3)若r=3![]() , PD=18, PC=27
, PD=18, PC=27![]() . 求△ABC各边长.
. 求△ABC各边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=45°,将△ABC绕点A逆时针方向旋转得△AEF,其中,E,F是点B,C旋转后的对应点,BE,CF相交于点D.若四边形ABDF为菱形,则∠CAE的大小是( )
![]()
A. 45°B. 60°C. 75°D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1).
(1)画出△ABC关于原点O成中心对称的图形△A1B1C1;
(2)在(1)的条件下直接写出点A1的坐标为______;B1的坐标为______;
(3)求出△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com