
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,OE⊥AB,OF⊥AC,垂足分别为E,F.求证:AB=AC;

(2)如图,若点O在△ABC的内部,求证:AB=AC;

(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.
【答案】(1)见解析;(2)见解析;(3)不一定成立,见解析.
【解析】
(1)求证AB=AC,就是求证∠B=∠C, 利用斜边直角边定理(HL)证明Rt△OEB≌Rt△OFC即可;
(2)首先得出Rt△OEB≌Rt△OFC,则∠OBE=∠OCF,由等边对等角得出∠OBC=∠OCB,进而得出∠ABC=∠ACB,由等角对等边即可得AB=AC;
(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC.
(1)证明: ∵点O在边BC上,OE⊥AB,OF⊥AC,点O到△ABC的两边AB,AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
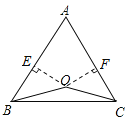
由题意知,OE=OF.∠BEO=∠CFO=90°,
∵在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠OBE=∠OCF,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)解:不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如示例图)


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
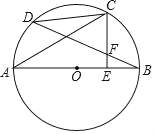
【题目】如图,AB是⊙O的直径,点C是弧BD的中点,CE⊥AB于点F.
(1)求证:BF=CF;
(2)若CD=3cm,AC=4cm,求⊙O的半径及CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>kx+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
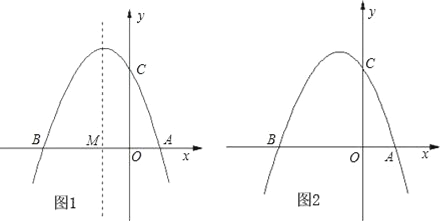
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接祖国七十周年庆典,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运16趟可完成,需支付运费5400元.已知甲、乙两车单独运完此垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟;
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com