
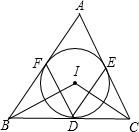
 已知⊙I为△ABC的内切圆,点D,E,F是切点,连接BI,CI,DE,DF,试猜想∠BIC与∠FDE有何数量关系,并证明你的猜想.
已知⊙I为△ABC的内切圆,点D,E,F是切点,连接BI,CI,DE,DF,试猜想∠BIC与∠FDE有何数量关系,并证明你的猜想. 分析 根据圆I是△ABC的内切圆求出∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB),根据三角形的内角和求得∠BIC=180°-(∠IBC+∠ICB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=90°+$\frac{1}{2}∠$A,连接IF、IE,求出∠FIE,即可求出∠EDF=$\frac{1}{2}$∠EIF=90°-$\frac{1}{2}∠$A,即可求出答案.
解答 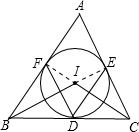 解:∵圆I是△ABC的内切圆,
解:∵圆I是△ABC的内切圆,
∴∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB,
∴∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A
∴∠BIC=180°-(∠IBC+∠ICB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=90°+$\frac{1}{2}∠$A,
连接IF、IE,
∵圆I是△ABC的内切圆,
∴∠IFA=∠IEA=90°,
∴∠FIE=360°-∠IFA-∠IEA-∠A=180°-∠A,
∴∠EDF=$\frac{1}{2}$∠EIF=90°-$\frac{1}{2}∠$A,
∴∠BIC+∠FDE=90°+$\frac{1}{2}∠$A+90°-$\frac{1}{2}∠$A=180°.
点评 本题主要考查对三角形的内角和定理,三角形的内切圆与内心,圆周角定理等知识点的理解和掌握,能熟练地运用性质进行推理是解此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
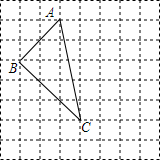 在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).
在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
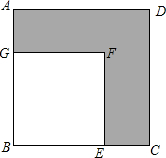 如图,工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG,若阴影部分面积为240mm2,AB=2x+8,BE=2x-4,求大正方形的边长.
如图,工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG,若阴影部分面积为240mm2,AB=2x+8,BE=2x-4,求大正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
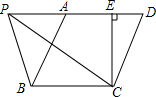 如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;
如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
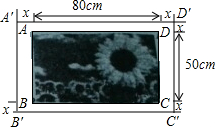 如图,在一幅长为80cm,宽为50cm的矩形画ABCD的四周镶一条金色纸边,制成一幅矩形挂图A′B′C′D′.如果金色镶边纸的宽度x为5cm,那么原风景画ABCD与矩形挂图A′B′C′D′是否相似?并说明理由.
如图,在一幅长为80cm,宽为50cm的矩形画ABCD的四周镶一条金色纸边,制成一幅矩形挂图A′B′C′D′.如果金色镶边纸的宽度x为5cm,那么原风景画ABCD与矩形挂图A′B′C′D′是否相似?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com