
����Ŀ����������ˮ���깺��һ����ˮ��������Ϊ 10 Ԫ/ǧ�ˣ��ۼ۲����� 10 Ԫ/ǧ�ˣ��Ҳ����� 16 Ԫ/ǧ�ˣ�����������������ָ�ˮ��һ��������� y��ǧ���� �������ۼ� x��Ԫ/ǧ�ˣ��������±���ʾ��һ�κ�����ϵ
������ y��ǧ�ˣ� | �� | 29 | 28 | 27 | 26 | �� |
�ۼ� x��Ԫ/ǧ�ˣ� | �� | 10.5 | 11 | 11.5 | 12 |
��1��ij������ˮ�����ۼ�Ϊ 14 Ԫ/ǧ�ˣ������ˮ������������
��2�����ij����������ˮ������ 100 Ԫ����ô����ˮ�����ۼ�Ϊ����Ԫ��
���𰸡���1�������ˮ����������Ϊ 22 ǧ������2������ˮ�����ۼ�Ϊ 15 Ԫ/ǧ�ˣ�
��������
��1�����ݱ����е����ݣ����ô���ϵ���������y��x֮��ĺ�����ϵʽ��������һ�κ���ͼ���ϵ���������������������x=14ʱy��ֵ��
��2������������=���ۼ�-�ɱ������������������ɵó�����x��һԪ���η��̣���֮���ɵó�x��ֵ���ٽ��10��x��16���ɵó����ۣ�
��1���� y �� x ֮��ĺ�����ϵʽΪ y=kx+b��k��0��������11��28������12��26������y=kx+b���ã�![]() ����ã�
����ã�![]() ��
��
��y �� x ֮��ĺ�����ϵʽΪ y=��2x+50�� �� x=14 ʱ��y=��2��14+50=22��
�൱���ˮ����������Ϊ 22 ǧ�ˣ�
��2����������ã���x��10������2x+50��=100�������ã�x2��35x+300=0��
��ã�x1=15��x2=20�� �֡�10��x��16��
��x=15��
�𣺸���ˮ�����ۼ�Ϊ 15 Ԫ/ǧ�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
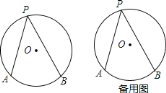
����Ŀ����ͼ��![]() ��
��![]() Ϊ
Ϊ![]() �ϵ��������㣬
�ϵ��������㣬![]() ��
��![]() �ϵĶ��㣨
�ϵĶ��㣨![]() ����
����![]() ��
��![]() �غϣ������dz�
�غϣ������dz�![]() Ϊ
Ϊ![]() �Ϲ��ڵ�
�Ϲ��ڵ�![]() ��
��![]() �Ļ����ǣ���֪
�Ļ����ǣ���֪![]() ��
��![]() �Ϲ��ڵ�
�Ϲ��ڵ�![]() ��
��![]() �Ļ����ǣ�
�Ļ����ǣ�
��1����![]() Ϊ
Ϊ![]() ��ֱ������
��ֱ������![]() ________��
________��
��2����![]() �뾶Ϊ
�뾶Ϊ![]() ��
��![]() ����
����![]() �Ķ�����
�Ķ�����
��3����![]() �뾶Ϊ
�뾶Ϊ![]() ��
��![]() ��
��![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
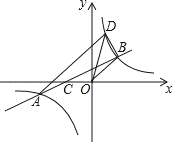
����Ŀ����ͼ����A�͵�B�ֱ��Ƿ���������y=![]() ��k��0��ͼ�������㣬����AB��x�Ḻ�����ڵ�C������BO��tan��BCO=
��k��0��ͼ�������㣬����AB��x�Ḻ�����ڵ�C������BO��tan��BCO=![]() ����BOC=135�㣬CO=2������A��AD��BO������������y=
����BOC=135�㣬CO=2������A��AD��BO������������y=![]() �ڵ�D������OD��BD��
�ڵ�D������OD��BD��
��1�����A�����ꣻ
��2������OBD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
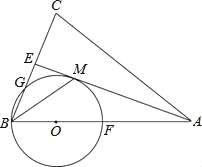
����Ŀ����ͼ������ABC�У�AB=AC��AE����BAC��ƽ���ߣ���ABC��ƽ���� BM��AE�ڵ�M����O��AB�ϣ��Ե�OΪԲ�ģ�OB�ij�Ϊ�뾶��Բ������M����BC�ڵ�G���� AB�ڵ�F��
��1����֤��AEΪ��O�����ߣ�
��2����BC=8��AC=12ʱ������O�İ뾶��
��3���ڣ�2���������£����߶�BG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
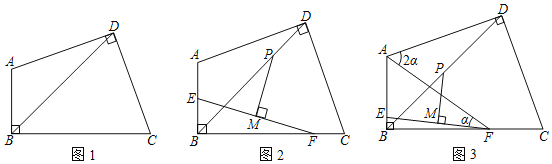
����Ŀ����ͼ1���ı���ABCD�У���ABC����ADC��90����AD��CD��
��1����֤��BDƽ�֡�ABC��
��2����ͼ2����E��F�ֱ���AB��BC�ϣ�����EF��M��EF���е㣬��M��EF�Ĵ��߽�BD��P����֤��AE+CF��![]() PD��
PD��
��3����ͼ3���ڣ�2�������£���AF����AE��CF����DAF��2��AFE��2����AF��13��BC��12![]() ����BC��AB������BD�ij���
����BC��AB������BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B(3��3)��˫����![]() (x>0)�ϣ���D��˫����
(x>0)�ϣ���D��˫����![]() (x<0)�ϣ���A�͵�C�ֱ���x�ᣬy����������ϣ��ҵ�A��B��C��D���ɵ��ı���Ϊ�����Σ�
(x<0)�ϣ���A�͵�C�ֱ���x�ᣬy����������ϣ��ҵ�A��B��C��D���ɵ��ı���Ϊ�����Σ�
��1����k��ֵ��
��3�����A�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1������ABCD�ڽ�����O����O�İ뾶Ϊ4��AB=4��������ABCD�Ƶ�O��ʱ����ת���õ�����A��B��C��D�䣬������A�䡢B�����ӻ���AD�ϻ���������ABCD�����A��B��C��D�佻�ڵ�M��N��G��H��
��1����AD��
��2���ж��ı���MNGH����״����˵�����ɣ�
��3������ת�������Ƿ�����ı���MNGH����������ֵ����Сֵ��������ڣ�����������������ڣ��Լ�Ҫ˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ADΪ��ABC�Ľ�ƽ���ߣ�DE��AB�ڵ�E��DF��AC�ڵ�F������EF��AD�ڵ�O��(1)��֤��AD��ֱƽ��EF��
(2)����BAC=![]() ��д��DO��AD֮���������ϵ������֤����
��д��DO��AD֮���������ϵ������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������
������![]()
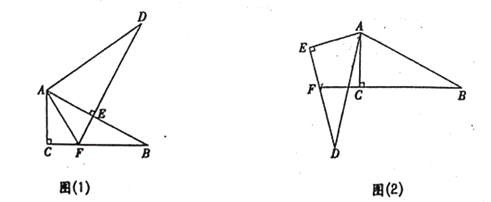
��1���۲췢�֣��������������ΰ�ͼ��1����ʾ�ķ�ʽ�ڷţ�ʹ��![]() ����
����![]() �ϣ�
�ϣ�![]() ���ӳ��߽�
���ӳ��߽�![]() �ڵ�
�ڵ�![]() ������
������![]() ����֤
����֤![]() ������ֱ��д��
������ֱ��д��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
��2�����̽������![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ��2����λ��ʱ��ʹ
��ת��ͼ��2����λ��ʱ��ʹ![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����1���еĽ��ۻ�������������������֤��������������д����ʱ
����1���еĽ��ۻ�������������������֤��������������д����ʱ![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com