
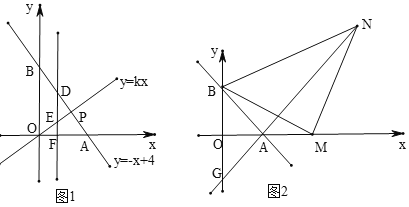
【题目】如图1,已知直线![]() 与坐标轴交于
与坐标轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,且
,且![]() 点的横坐标是纵坐标的
点的横坐标是纵坐标的![]() 倍.
倍.
(1)求![]() 的值.
的值.
(2)![]() 为线段
为线段![]() 上一点,
上一点,![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 点坐标.
点坐标.
(3)如图2,![]() 为
为![]() 点右侧
点右侧![]() 轴上的一动点,以
轴上的一动点,以![]() 为直角顶点,
为直角顶点,![]() 为腰在第一象限内作等腰直角
为腰在第一象限内作等腰直角![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,当
,当![]() 点运动时,
点运动时,![]() 点的位置是否发生变化?若不变,请求出它的坐标;如果变化,请说明理由.
点的位置是否发生变化?若不变,请求出它的坐标;如果变化,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不变,G(0,-4).
;(3)不变,G(0,-4).
【解析】
(1)根据P点的横坐标是纵坐标的3倍,可得k的值;
(2)由图象可知,D、E、F三点在同一条直线上,横坐标相同,可设D、E点横坐标,分别代入解析式可以表示出纵坐标,进而表示出DE、EF的长度,从而构造出方程,求出点D坐标.
(3)过![]() 作
作![]() 轴于
轴于![]() ,根据题目条件,先证明
,根据题目条件,先证明![]() ,进而能够得到AH=NH,得到
,进而能够得到AH=NH,得到![]() 为等腰直角三角形,然后得到
为等腰直角三角形,然后得到![]() 也是等腰三角形,进而得到G点的坐标.
也是等腰三角形,进而得到G点的坐标.
解:(1) ![]() 直线
直线![]() 上点P的横坐标是纵坐标的3倍,
上点P的横坐标是纵坐标的3倍,
![]() 若P点纵坐标为a则横坐标为3a,
若P点纵坐标为a则横坐标为3a,
![]()
![]() ,
,
![]()
![]() ;
;
(2)设D点横坐标为m,则D点坐标为![]() ,
,
![]() DF=
DF= ![]()
![]() 轴于F交
轴于F交![]() 于E,
于E,
![]() E点坐标为
E点坐标为![]()
![]() EF=
EF= ![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
解得:![]()
![]()
![]()
(3)![]() 点的位置不发生变化,
点的位置不发生变化,![]() .
.
过![]() 作
作![]() 轴于
轴于![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
又![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
∴G(0,-4).


科目:初中数学 来源: 题型:
【题目】某班要购买6副乒乓球拍和![]() 盒(
盒(![]() )乒乓球,甲、乙两家商店定价都为乒乓球拍每副50元,乒乓球每盒10元,现两家商店都搞促销活动,甲店优惠方案是:每买一副乒乓球拍送一盒乒乓球,乙店优惠方案是:按定价的9折出售.
)乒乓球,甲、乙两家商店定价都为乒乓球拍每副50元,乒乓球每盒10元,现两家商店都搞促销活动,甲店优惠方案是:每买一副乒乓球拍送一盒乒乓球,乙店优惠方案是:按定价的9折出售.
(1)用含![]() 的代数式表示:该班在甲店购买时需付款____________元;在乙店购买时需付款____________元,(所填式子需化为最简形式).
的代数式表示:该班在甲店购买时需付款____________元;在乙店购买时需付款____________元,(所填式子需化为最简形式).
(2)当![]() 时,到哪家店子购买比较合算?说明理由.
时,到哪家店子购买比较合算?说明理由.
(3)若要你去甲、乙两家商店购买6副球拍和10盒乒乓球,你最少要付多少钱?并写出你的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
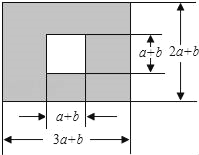
【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
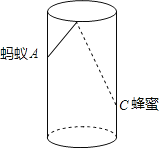
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
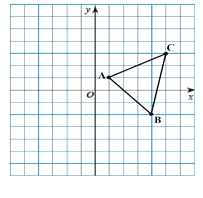
【题目】如图,在平面直角坐标系中, ABC 三个顶点的坐标分别为 A(1,1) , B(4, 2) ,C (5, 3) .
(1)在图中画出 ABC 关于 y 轴的对称 图形 A1B1C1 ;(要求:画出三角形,标出相应顶点的 字母,不写结论)
(2)分别写出A1B1C1 三个顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com