

ЗжЮі ЃЈ1ЃЉПЩвдгЩЗНГЬзщ$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{2}X+6}\end{array}\right.$ЕФНтЕУЕННЛЕуBЕФзјБъЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНПЩвдЧѓЁїAOBУцЛ§ЃЎ
ЃЈ2ЃЉЂйИљОнЕуEдкABЩЯЃЌРћгУЯрЫЦШ§НЧаЮЃЌПЩвдШЗЖЈtЕФжЕЃЎ
ЂкЯШМйЩшЕуFдкжБЯпABЩЯЪБЃЌРћгУЯрЫЦШ§НЧаЮЧѓГіtЕФжЕЃЌНјЖјШЗЖЈЕуFЕФзјБъЃЌОЭПЩвдХаЖЯЕуFгыЕуBЪЧЗёжиКЯЃЎ
ЃЈ3ЃЉЯШЛГіЭМЯѓЃЌгаСНжжЧщаЮЃЌдйРћгУЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌЧѓГіжиЕўВПЗжЕФУцЛ§ЃЎ
ЃЈ4ЃЉИљОнОиаЮЕФаджЪвдМАОиаЮУцЛ§ЙЋЪНЃЌСаГіЙигкtЕФВЛЕШЪНЃЌШЛКѓЧѓГіtЕФЗЖЮЇЃЎ
НтД№ НтЃКЃЈ1ЃЉЕБy=0ЪБЃЌ-$\frac{1}{2}$x+6=0ЕУx=12ЃЌЙЪAЃЈ12ЃЌ0ЃЉЃЌ
гЩ$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{2}x+6}\end{array}\right.$ЕУ$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$ЃЌЙЪBЃЈ4ЃЌ4ЃЉЃЌ
SЁїABO=$\frac{1}{2}ЁС12ЁС4$=24ЃЌ
ЙЪД№АИЗжБ№ЮЊBЃЈ4ЃЌ4ЃЉЃЌSЁїABO=24ЃЎ
ЃЈ2ЃЉЭМ1жаЃЌЕБЕуEдкABЩЯЪБЃЌЩшжБЯпABгыyжсНЛгкЕуKЃЌвзжЊkЃЈ0ЃЌ6ЃЉЃЌ
ЁпEDЁЮKOЃЌ
Ёр$\frac{ED}{KO}=\frac{AD}{AO}$ЃЌ
Ёр$\frac{2t}{6}=\frac{6-t}{12}$ЃЌ
Ёрt=$\frac{6}{5}$ЃЌ
ЁрЕуEдкжБЯпABЩЯЪБЃЌt=$\frac{6}{5}$ЃЎ
ЭМ2жаЃЌЕБЕуFдкABЩЯЪБЃЌ
ЁпFCЁЮOKЃЌ
Ёр$\frac{FC}{KO}$=$\frac{AC}{AO}$ЃЌ
Ёр$\frac{2t}{6}=\frac{6+t}{12}$ЃЌ
Ёрt=2ЃЌ
ЁрFC=2t=4ЃЌAC=6+t=8ЃЌ
ЁрOC=OC-AC=12-8=4ЃЌ
ЁрЕуFзјБъЮЊFЃЈ4ЃЌ4ЃЉЃЌ
ЁпBЃЈ4ЃЌ4ЃЉЃЌ
ЁрЕуFгыЕуBжиКЯЃЌ
ЁрдкдЫЖЏЙ§ГЬжаЃЌЕуFФмгыЕуBжиКЯЃЎ
ЃЈ3ЃЉгыЃЈ2ЃЉПЩжЊЕБ$\frac{6}{5}$ЃМtЃМ2Лђ2ЃМtЃМ6ЪБЃЌе§ЗНаЮCDEFгыЁїABOжиЕўВПЗжЪЧЮхБпаЮЃЎМћЭМ3ЁЂЭМ4ЃЎ
дкЭМ3жаЃЌе§ЗНаЮEFCDЕФБпEFНЛABгкNЃЌБпEDНЛABгкHЃЌ
ЁпDHЁЮKOЃЌ
Ёр$\frac{HD}{KO}$=$\frac{AD}{AO}$ЃЌ
Ёр$\frac{HD}{6}=\frac{6-t}{12}$ЃЌ
ЁрHD=$\frac{1}{2}ЃЈ6-tЃЉ$ЃЌEH=2t-$\frac{1}{2}$ЃЈ6-tЃЉ=$\frac{5}{2}$t-3ЃЌ
ЁпNEЁЮADЃЌ
ЁрЁїENHЁзЁїDAHЃЌ
Ёр$\frac{EN}{AD}=\frac{EH}{HD}$ЃЌ
ЁрEN=5t-6ЃЌ
ЁрS=ЃЈ2tЃЉ2-$\frac{1}{2}$•ЃЈ5t-6ЃЉ•ЃЈ$\frac{5}{2}t-3$ЃЉ=-$\frac{9}{4}{t}^{2}$+15t-9
ЃЈ$\frac{6}{5}ЃМtЃМ2$ЃЉ
дкЭМ4жаЃЌS=SЁїAOB-SЁїOCN-SЁїADH
=$\frac{1}{2}$ЁС12ЁС4-$\frac{1}{2}$•ЃЈ6-tЃЉ2-$\frac{1}{2}$•ЃЈ6-tЃЉ$•\frac{1}{2}ЃЈ6-tЃЉ$
=24-27+9t-$\frac{3}{4}$t2
=-$\frac{3}{4}$t2+9t-3
ЃЈ2ЃМtЃМ6ЃЉ
злЩЯЫљЪіSгыtЙиЯЕЃКS=$\left\{\begin{array}{l}{-\frac{9}{4}{t}^{2}+15t-9}&{ЃЈ\frac{6}{5}ЃМtЃМ2ЃЉ}\\{-\frac{3}{4}{t}^{2}+9t-3}&{ЃЈ2ЃМtЃМ6ЃЉ}\end{array}\right.$ЃЎ
ЃЈ4ЃЉЭМ5жаЃЌжБЯпEFНЛBHгкPЃЌжБЯпBHНЛOAгкLЃЌFCНЛHNгкKЃЌ
ЁпBЁЂHЙигкжБЯпEFЖдГЦЃЌBЁЂGЙигкжБЯпFCЖдГЦЃЌ
ЁрBP=PH=|4-2t|ЃЌHK=HN=|6-t-4|ЃЌ
ЁрSжиЕў=|6-t-4|•|4-2t|ЃМ$\frac{9}{8}$
ЁрЃЈt-2ЃЉ2ЃМ$\frac{9}{16}$
Ёр|t-2|ЃМ$\frac{3}{4}$
Ёр-$\frac{3}{4}$ЃМt-2ЃМ$\frac{3}{4}$ЃЌ
Ёр$\frac{5}{4}$ЃМtЃМ$\frac{11}{4}$ЃЎ
ЕуЦР БОЬтПМВщСЫвЛДЮКЏЪ§ЕФЭМЯѓгыаджЪЁЂЯрЫЦаЮШ§НЧаЮЕФХаЖЈгыаджЪвдМАЖрБпаЮУцЛ§ЕФЧѓЗЈЃЌЪЧвЛЕРдЫЖЏаЭзлКЯЬтЃЌЩцМАЕНЖЏЕуаЭЃЈСНИіЖЏЕуЃЉКЭЖЏЯпаЭЃЌдЫЖЏЙ§ГЬИДдгЃЌФбЖШЦФДѓЃЌЖдЭЌбЇУЧЕФНтЬтФмСІвЊЧѓКмИпЃЎЖСЖЎЬтвтЃЌХЊЧхЖЏЕугыЖЏЯпЕФдЫЖЏЙ§ГЬЃЌЪЧНтЬтЕФвЊЕуЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЃЈ0ЃЌ8ЃЉЁЂЕуBЃЈ6ЃЌ8ЃЉЃЎЕуPЭЌЪБТњзуЯТУцСНИіЬѕМўЃКЂйЕуPЕНAЁЂBСНЕуЕФОрРыЯрЕШЃЛЂкЕуPЕНЁЯxOyЕФСНБпЕФОрРыЯрЕШЃЎ
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЃЈ0ЃЌ8ЃЉЁЂЕуBЃЈ6ЃЌ8ЃЉЃЎЕуPЭЌЪБТњзуЯТУцСНИіЬѕМўЃКЂйЕуPЕНAЁЂBСНЕуЕФОрРыЯрЕШЃЛЂкЕуPЕНЁЯxOyЕФСНБпЕФОрРыЯрЕШЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 30Ёу | BЃЎ | 45Ёу | CЃЎ | 60Ёу | DЃЎ | 90Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌЯвCDЁЭABгкHЃЌЯвCEЁЭBDгкGЃЌНЛABгкЕуFЃЌЯТСаНсТлВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌЯвCDЁЭABгкHЃЌЯвCEЁЭBDгкGЃЌНЛABгкЕуFЃЌЯТСаНсТлВЛе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ| AЃЎ | CH=DH | BЃЎ | AH=FH | CЃЎ | CD=CE | DЃЎ | CF=DE |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
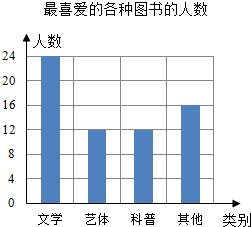 ФГаЃЁАЗХЗЩУЮЯыЁБЖСЪщаЁзщажњРЯЪІЫцЛњГщШЁБОаЃЕФВПЗжбЇЩњЃЌЕїВщЫћУЧзюЯВАЎЕФЭМЪщРрБ№ЃЈЭМЪщЗжЮЊЮФбЇРрЁЂвеЬхРрЁЂПЦЦеРрЁЂЦфЫћЕШЫФРрЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМЃЌдђБЛЕїВщЕФбЇЩњжаЯВАЎЮФбЇРрЁЂвеЬхРрЁЂПЦЦеРрЕФЙВга48ШЫЃЎ
ФГаЃЁАЗХЗЩУЮЯыЁБЖСЪщаЁзщажњРЯЪІЫцЛњГщШЁБОаЃЕФВПЗжбЇЩњЃЌЕїВщЫћУЧзюЯВАЎЕФЭМЪщРрБ№ЃЈЭМЪщЗжЮЊЮФбЇРрЁЂвеЬхРрЁЂПЦЦеРрЁЂЦфЫћЕШЫФРрЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМЃЌдђБЛЕїВщЕФбЇЩњжаЯВАЎЮФбЇРрЁЂвеЬхРрЁЂПЦЦеРрЕФЙВга48ШЫЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЪЧжаЙњЯѓЦхЦхХЬЕФвЛВПЗжЃЌШє
ШчЭМЪЧжаЙњЯѓЦхЦхХЬЕФвЛВПЗжЃЌШє ЮЛгкЕуЃЈ1ЃЌ-1ЃЉЃЌдђ
ЮЛгкЕуЃЈ1ЃЌ-1ЃЉЃЌдђ ЮЛгкЕуЃЈЁЁЁЁЃЉ
ЮЛгкЕуЃЈЁЁЁЁЃЉ| AЃЎ | ЃЈ3ЃЌ-2ЃЉ | BЃЎ | ЃЈ2ЃЌ-3ЃЉ | CЃЎ | ЃЈ-2ЃЌ3ЃЉ | DЃЎ | ЃЈ-3ЃЌ2ЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌЁїABCжаЃЌЁЯABC=90ЁуЃЌЁЯC=30ЁуЃЌADЪЧНЧЦНЗжЯпЃЌDEЁЭACгкEЃЌADЁЂBEЯрНЛгкЕуFЃЌдђЭМжаЕФЕШбќШ§НЧаЮгаЃЈЁЁЁЁЃЉ
ШчЭМЃЌЁїABCжаЃЌЁЯABC=90ЁуЃЌЁЯC=30ЁуЃЌADЪЧНЧЦНЗжЯпЃЌDEЁЭACгкEЃЌADЁЂBEЯрНЛгкЕуFЃЌдђЭМжаЕФЕШбќШ§НЧаЮгаЃЈЁЁЁЁЃЉ| AЃЎ | 2Иі | BЃЎ | 3Иі | CЃЎ | 4Иі | DЃЎ | 5Иі |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
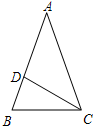 ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌDЮЊABЩЯвЛЕуЃЌAD=CDЃЌШєЁЯACD=40ЁуЃЌдђЁЯB=70ЁуЃЎ
ШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌDЮЊABЩЯвЛЕуЃЌAD=CDЃЌШєЁЯACD=40ЁуЃЌдђЁЯB=70ЁуЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com