
分析 (1)考虑点M在原点右边或左边两种情形即可.
(2)分三种情形讨论,①当AM1=BM1时,求出直线AB的垂直平分线HM1为y=2x-3,即可解决问题,②AB=AM2时,③当BA=BM3时根据等腰三角形定义即可解决.
解答 解:(1)如图1中,当0<t≤4时,s=$\frac{1}{2}$•OM•CO=2(4-t)=-2t+8,
当t>4时,s=$\frac{1}{2}$•OM′•CO=2(t-4)=2t-8,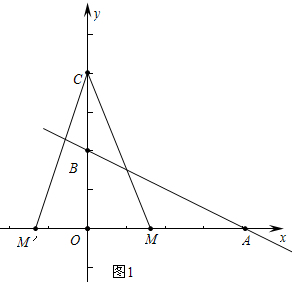
(2)如图2中,①当AM1=BM1时,直线AB的垂直平分线HM1为y=2x-3,所以点M1坐标为($\frac{3}{2}$,0).
②AB=AM2时,点M2(4-2$\sqrt{5}$,0).
③当BA=BM3时,点M3(-4,0).
综上所述点M坐标为($\frac{3}{2}$,0)或(-4,0)或(4-2$\sqrt{5}$,0).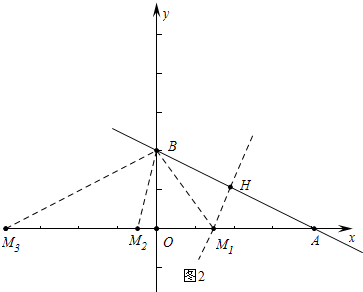
点评 本题考查一次函数的有关知识、勾股定理、等腰三角形的定义等知识,学会分类讨论的思想,容易漏解,解题的关键是正确画出图形,属于中考常考题型.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
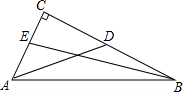 如图,在△ABC中,∠C=90°,AD,BE是中线,BE=2$\sqrt{10}$,AD=5,求AB的长(提示:设CE=x,CD=y).
如图,在△ABC中,∠C=90°,AD,BE是中线,BE=2$\sqrt{10}$,AD=5,求AB的长(提示:设CE=x,CD=y).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李大叔带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示.结合图形解答下列问题
李大叔带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示.结合图形解答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
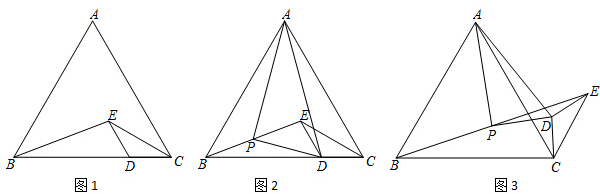
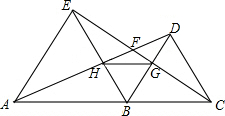 已知点A、B、C三点共线,分别以线段AB、BC为边作等边△ABE,△DBC,连接AD、EC.
已知点A、B、C三点共线,分别以线段AB、BC为边作等边△ABE,△DBC,连接AD、EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com