
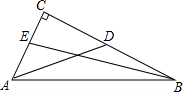
 如图,在△ABC中,∠C=90°,AD,BE是中线,BE=2$\sqrt{10}$,AD=5,求AB的长(提示:设CE=x,CD=y).
如图,在△ABC中,∠C=90°,AD,BE是中线,BE=2$\sqrt{10}$,AD=5,求AB的长(提示:设CE=x,CD=y). 分析 设CE=x,CD=y,根据三角形中线的定义可得AC=2x,BC=2y,然后利用勾股定理列式整理求出x2+y2,再利用勾股定理解答即可.
解答 解:设CE=x,CD=y,
∵AD、BE是Rt△ABC的中线,
∴AC=2x,BC=2y,
在Rt△ACD中,CD2+AC2=AD2,
∴(2x)2+y2=52,即4x2+y2=25①,
在Rt△BCE中,BC2+CE2=BE2,
∴(2y)2+x2=(2$\sqrt{10}$)2,
即4y2+x2=40②,
由①②得:x2+y2=13,
在Rt△ABC中,由勾股定理得,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{4{x}^{2}+4{y}^{2}}$=2$\sqrt{13}$.
点评 本题考查了勾股定理,三角形的中线的定义;熟练掌握勾股定理,通过设未知数由勾股定理求出x2+y2=13是解题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:选择题
| A. | 火车在笔直的轨道上匀速行驶 | B. | 商场电梯上上下下运动 | ||
| C. | 滑雪运动员在平坦的雪地上滑行 | D. | 汽车玻璃上雨刷器的运动 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
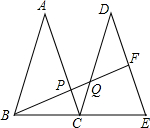 如图,△ABC和△DCE是两个全等的等腰三角形,底边BC、CE在一条直线上,F为DE的中点,连接BF,交AC于点P,交DC于点Q,则$\frac{PQ}{PB}$的值等于$\frac{1}{3}$.
如图,△ABC和△DCE是两个全等的等腰三角形,底边BC、CE在一条直线上,F为DE的中点,连接BF,交AC于点P,交DC于点Q,则$\frac{PQ}{PB}$的值等于$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com