
【题目】已知关于![]() 的方程
的方程![]() 有两个实数根
有两个实数根![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() ,求
,求![]() 的值;
的值;
【答案】(1)![]() ;(2)k=-3
;(2)k=-3
【解析】
(1)依题意得△≥0,即[-2(k-1)]2-4k2≥0;(2)依题意x1+x2=2(k-1),x1·x2=k2
以下分两种情况讨论:①当x1+x2≥0时,则有x1+x2=x1·x2-1,即2(k-1)=k2-1;②当x1+x2<0时,则有x1+x2=-(x1·x2-1),即2(k-1)=-(k2-1);
解:(1)依题意得△≥0,即[-2(k-1)]2-4k2≥0
解得![]()
(2)依题意x1+x2=2(k-1),x1·x2=k2
以下分两种情况讨论:
①当x1+x2≥0时,则有x1+x2=x1·x2-1,即2(k-1)=k2-1
解得k1=k2=1
∵![]()
∴k1=k2=1不合题意,舍去
②当x1+x2<0时,则有x1+x2=-(x1·x2-1),即2(k-1)=-(k2-1)
解得k1=1,k2=-3
∵![]()
∴k=-3
综合①、②可知k=-3


科目:初中数学 来源: 题型:
【题目】如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.
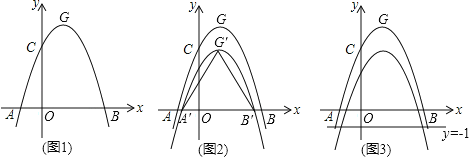
(1)求出抛物线C1的解析式,并写出点G的坐标;
(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.

(1)求抛物线的解析式及A点坐标.
(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.
(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′、B′D
①当点B′落坐标轴上时,求点D的坐标.
②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月饼是久负盛名的中国传统糕点之一,宋代大诗人苏东坡有诗句“小饼如嚼月,中有酥和饴”赞美月饼.为满足市场需求,某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不低于45元且不超过58元,根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量![]() (盒)与每盒售价
(盒)与每盒售价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个抛物线形的拱形桥洞,桥面离水面的距离为5.6米,桥洞离水面的最大高度为![]() ,跨度为
,跨度为![]() ,如图所示,把它的图形放在直角坐标系中.
,如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式.
(2)如图,在对称轴右边![]() 处,桥洞离桥面的高是多少?
处,桥洞离桥面的高是多少?
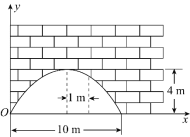
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、 F分别为边AB、CD的中点,BD是对角线.过点有作AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若∠G=90° ,求证:四边形DEBF是菱形.
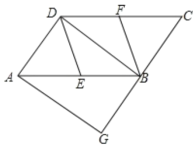
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 为正比例函数
为正比例函数![]() 的图象,点
的图象,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 轴于点
轴于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ;过点
;过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,…,按此规律操作下所得到的正方形
,…,按此规律操作下所得到的正方形![]() 的面积是
的面积是
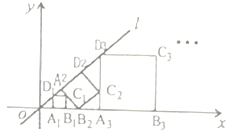
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
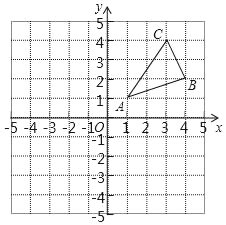
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com