练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若一种服装销售盈利y万元与销售量x万件满足函数表达式y=-2x2+4x+5，则盈利最大值是
     
    ．
    考点：二次函数的应用
    专题：
    分析：利用配方法求出二次函数最值进而得出答案．
    解答：解：y=-2x2+4x+5
    =-2（x2-2x）+5
    =-2[（x-1）2-1]+5
    =-2（x-1）2+7，
    则盈利最大值为：7万元．
    故答案为：7万元．
    点评：此题主要考查了二次函数的应用，熟练应用配方法求出二次函数最值是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知直线AB分别与x轴、y轴交于点B、点A，且经过（2，-2）和（-1，4）两点，将这条直线向左平移与x轴、y轴分别交于点C、点D，若DB=DC，求直线CD的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将下列式子化为度：
    （1）56°24′=
     
    °；
    （2）25°36′12″×4=
     
    °；
    （3）104°24′÷6=
     
    °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    同一个圆的中内接正六边形与其外切正六边形的周长比是
     
    ，面积比是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知AB=AC=BD，那么（　　）
    A、∠1=∠2
    B、2∠1+∠2=180°
    C、∠1+3∠2=180°
    D、3∠1-∠2=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）先观察下列等式，再完成题后问题：
    1
    2×3
    =
    1
    2
    -
    1
    3
      
    1
    3×4
    =
    1
    3
    -
    1
    4
      
    1
    4×5
    =
    1
    4
    -
    1
    5

    ①请你猜想：
    1
    2010×2011
    =
     
    ；
    ②若a、b为有理数，且|a-1|+（ab-2）2=0，求：
    1
    ab
    +
    1
    (a+1)(b+1)
    +
    1
    (a+2)(b+2)
    +…+
    1
    (a+2009)(b+2009)
    的值．
    （2）如图，把一个面积为1的正方形等分成两个面积为
    1
    2
    的长方形，接着把面积为
    1
    2
    的长方形等分成两个面积为
    1
    4
    的正方形，再把面积为
    1
    4
    的正方形等分成两个面积为
    1
    8
    的矩形．如此进行下去，试利用图形揭示的规律计算：
    1
    2
    +
    1
    4
    +
    1
    8
    +
    1
    16
    +
    1
    32
    +
    1
    64
    +
    1
    128
    +
    1
    256
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

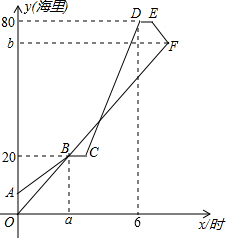    在距离港口80海里处，有一艘渔船发出求救信息，甲、乙两艘救援船同时接到救援任务，甲船立即出发，乙船因需要等候救援家属，在甲救援船驶离港口5海里时才出发．乙船以10海里/小时的速度匀速行驶，甲船途中因故障维修停船1小时，然后提高速度匀速行驶，到达目的地救援1小时后原路匀速返回与乙船相遇，甲船返回时的速度与提高后的速度相同，图中折线AB-BC-CD-DE-EF，线段OF分别表示甲、乙两船与港口的距离y（海里）与乙船出发时间x（时）之间的图象．
    （1）求a的值；
    （2）乙船出发多长时间与甲船相遇？
    （3）求b的值；
    （4）请直接写出在两船第三次相遇前，两船相距10海里时的所有x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列说法不正确的是（　　）
    A、一组邻边相等的矩形是正方形
    B、对角线相等的菱形是正方形
    C、对角线互相垂直的矩形是正方形
    D、对角线互相垂直且相等的四边形是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    阅读材料：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”．我们可得出一种计算三角形面积的新方法：S△ABC=
    1
    2
    ah，即三角形面积等于水平宽与铅垂高乘积的一半．解答下列问题：如图2，抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），交y轴于点B．
    （1）求抛物线和直线AB的解析式；
    （2）求△CAB的铅垂高CD及S△CAB；
    （3）抛物线上是否存在一点P，使S△PAB=
    9
    8
    S△CAB？若存在，求出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案