
【题目】已知关于x的一元二次方程x2﹣3x+m﹣2=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2满足2x1=|x2|+1,求m的值.
【答案】(1)m≤![]() (2)
(2)![]() 或﹣8
或﹣8
【解析】
(1)根据根的判别式即可求解;
(2)根据根与系数的关系,分情况讨论即可求得m的值.
解:(1)∵关于x的一元二次方程x2﹣3x+m﹣2=0有两个实数根,
∴△≥0,即9﹣4(m﹣2)≥0
解得m≤![]() .
.
答:m的求值范围为m≤![]() .
.
(2))根据根与系数的关系:
x1+x2=3,x1x2=m﹣2,
∵x1,x2满足2x1=|x2|+1,
①当x2≥0时,2x1=x2+1
把x2=3﹣x1代入,得
2x1=3﹣x1+1
解得x1=![]() ,
,
∴x2=![]() ,
,
∴m﹣2=x1x2=![]()
∴m=![]() .
.
②当x2≤0时,2x1=﹣x2+1
∴2x1+3﹣x1=1
解得x1=﹣2,x2=5,
∴m﹣2=﹣10
m=﹣8.
答:m的值为![]() 或﹣8
或﹣8


科目:初中数学 来源: 题型:
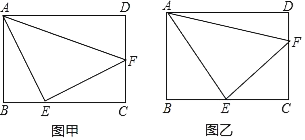
【题目】在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°.如图甲,若EA=EF,则EF=_____;如图乙,若CE=CF,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=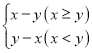 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标 ;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形,它反映了图形中点的个数与第![]() 个图形之间的某种变化规律.
个图形之间的某种变化规律.
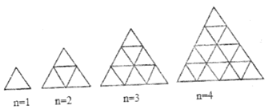
(1)填写下表:
第 | 1 | 2 | 3 | 4 | … |
图形中所有点的个数 | … |
(2)设第![]() 个图形中点的个数是
个图形中点的个数是![]() 个,试写出
个,试写出![]() 与
与![]() 的关系式 .
的关系式 .
(3)若某个图形中所有点的个数是66个,求这是第几个图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
|
| m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
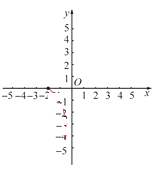
(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,经过点(-1,0),有下列结论:①abc<0;②a+c>b;③3a+c=0;④a+b>m(am+b)(其中m≠1)其中正确的结论有( )
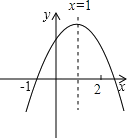
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
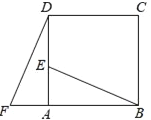
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=3,AB=7,
求(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
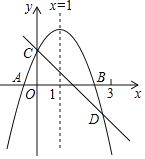
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,则下列结论:
①abc>0
②a﹣b+c<0;
③2a+b+c>0;
④x(ax+b)≤a+b;
其中正确的有_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据农业部提出“大力发展农村产业,实现乡村全面振兴”的方针,我市精确扶贫,指导某县大力发展大五星枇杷种植,去年、今年枇杷产量连续获得大丰收,该县枇杷销售采用线下销售和线上销售两种模式.
(1)今年该县种植专业户大五星枇杷产量为4500千克,全部售出,其中线上销售量不超过线下销售的4倍,求该种植专业户线下销售量至少多少千克?
(2)该种植专业户去年大五星枇杷线下销售均价为10元/千克,销售量为900千克,线上销售均价为8元/千克,销售量为1800千克,今年线下销售均价上涨![]() ,但销售量下降了
,但销售量下降了![]() ,线上销售均价上涨了
,线上销售均价上涨了![]() ,销量与去年持平,今年大五星枇杷的销售总额比去年销售总额减少了
,销量与去年持平,今年大五星枇杷的销售总额比去年销售总额减少了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com