
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD.CE∥AB,连接DE交AC于F.
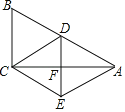
(1)证明:四边形ADCE是菱形;
(2)试判断BC与线段EF的关系,并说明理由.
【答案】(1)见解析;(2)结论:BC∥EF,BC=2EF,理由见解析
【解析】
(1)先根据两组对边分别平行的四边形是平行四边形证明四边形ADCE是平行四边形,
根据邻边相等的平行四边形是菱形即可证明.
(2)结论:BC∥EF,BC=2EF.利用菱形的性质以及三角形的中位线定理即可解决问题.
(1)证明:∵AE∥CD,EC∥AD,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,BD=AD,
∴CD=AD=BD,
∴四边形ADCE是菱形.
(2)解:结论:BC∥EF,BC=2EF.
理由:∵四边形ADCE是菱形,
∴DE⊥AC,DF=EF,
∴∠DFA=∠ACB=90°,
∴DE∥BC,
∵BD=AD,
∴CF=FA,
∴BC=2DF=2EF.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
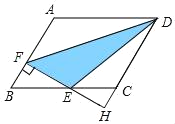
【题目】如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“七·一”党的生日,某校准备组织师生共310人参加一次大型公益活动,租用4辆大客车和6辆小客车恰好全部坐满,已知每辆大客车的座位数比小客车多15个.
(1)求每辆大客车和小客车的座位数;
(2)经学校统计,实际参加活动人数增加了40人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为使所有参加活动的师生均有座位,最多租用小客车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)请求出抛物线的解析式;
(2)当0<x<4时,请直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇风力资源丰富,为了实现低碳环保,该乡镇决定开展风力发电,打算购买10台风力发电机组.现有A,B两种型号机组,其中A型机组价格为12万元/台,月均发电量为2.4万kw.h;B型机组价格为10万元/台,月均发电量为2万kw.h.经预算该乡镇用于购买风力发电机组的资金不高于105万元.
(1)请你为该乡镇设计几种购买方案;
(2)如果该乡镇用电量不低于20.4万kw.h/月,为了节省资金,应选择那种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
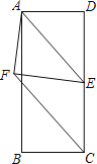
【题目】 如图,在矩形ABCD中,AB=8,AD=3,点E是CD的中点,连接AE,将△ADE沿直线AE折叠,使点D落在点F处,则线段CF的长度是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com