
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC=![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.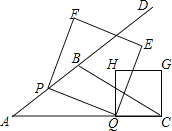
【答案】(1)![]() ;(2)S最小值=
;(2)S最小值=![]() ;(3)
;(3)![]() ;
; ![]() ;1;
;1; ![]() .
.
【解析】试题分析:(1)如图1,过点B作BM⊥AC于点M,利用面积法求得BM的长度,利用勾股定理得到AM的长度,最后由锐角三角函数的定义进行解答;
(2)如图2,过点P作PN⊥AC于点N.利用(1)中的结论和勾股定理得到PN2+NQ2=PQ2,所以由正方形的面积公式得到S关于t的二次函数,利用二次函数的顶点坐标公式和二次函数图象的性质来求其最值;
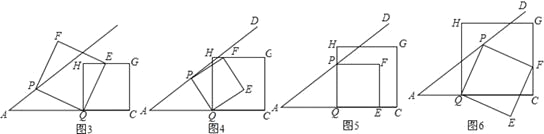
(3)需要分类讨论:当点E在边HG上、点F在边HG上、点P边QH(或点E在QC上)、点F边C上时相对应的t的值.
试题解析:(1)如图1,过点B作BM⊥AC于点M,
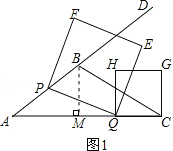
∵AC=9,S△ABC=![]() ,
,
∴![]() ACBM=
ACBM=![]() ,即
,即![]() ×9BM=
×9BM=![]() ,
,
解得BM=3.
由勾股定理,得
AM=![]() =4,
=4,
则tanA=![]() ;
;
(2)存在.如图2,过点P作PN⊥AC于点N.依题意得AP=CQ=5t.
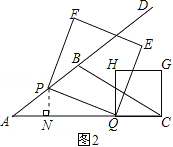
∵tanA=![]() ,
,
∴AN=4t,PN=3t.
∴QN=AC﹣AN﹣CQ=9﹣9t.
根据勾股定理得到: ![]() ,
,
S正方形PQEF= ![]() =
=![]() ﹣162t+81(0<t<
﹣162t+81(0<t<![]() ).
).
∵﹣![]() 在t的取值范围之内,
在t的取值范围之内,
∴S最小值=![]() ;
;
(3)①如图3,当点E在边HG上时,t1=![]() ;
;
②如图4,当点F在边HG上时,t2=![]() ;
;
③如图5,当点P在边QH(或点E在QC上)时,t3="1"
④如图6,当点F在边C上时,t4=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y1=2x与双曲线y2= ![]() 的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<﹣1.”你同意他的观点吗? 答: . 理由是 .
的图象如图所示,小明说:“满足y1<y2的x的取值范围是x<﹣1.”你同意他的观点吗? 答: . 理由是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年6月17日北京国际自行车大会召开,来自世界各地的4000多名骑游爱好者齐聚夏都延庆.各种自行车赛事也带动了延庆的骑游产业.据调查,延庆区某骑游公司每月的租赁自行车数的增长率相同,今年四月份的骑游人数约为9000人,六月份的骑游人数约为16000人,求该骑游公司租赁自行车数的月平均增长率(精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
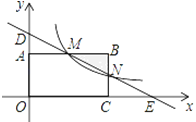
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数y=![]() (x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com